Учет размеров и эффективности детектора
При малых размерах счетчика (сцинтилляторы) можно считать, что его показания отражают реальную картину пространственного изменения плотности потока излучения. При применении протяженных («длинных») счетчиков, длина которых соизмерима с длиной свободного пробега частиц, амплитуда поля может существенно изменяться по длине детектора. Показания таких детекторов пропорциональны средней по объему счетчика амплитуде поля. Закон усреднения задается пространственной эффективностью детектора 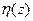 , под которой понимается вероятность регистрации в единице объема счетчика.
, под которой понимается вероятность регистрации в единице объема счетчика.
Для интерпретации результатов измерений необходимо знать истинное распределение поля, восстановив его по измерениям интегрирующим детектором.
Общий метод решения задачи восстановления полей по их интегральным характеристикам был предложен Ш.А.Губерманом и Д.А.Кожевниковым[1]. Для одномерной задачи функциональная связь между амплитудой измеренного поля Ф(z,l) и истинного Ф(z) имеет вид:
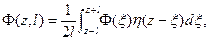 (7.41)
(7.41)
где z – координата глубины; x - текущая координата: l - полудлина счетчика; 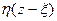 - эффективность регистрации частиц по длине счетчика. При равномерной эффективности
- эффективность регистрации частиц по длине счетчика. При равномерной эффективности
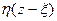 = (7.42)
= (7.42)
При этом выражение (7.41) принимает вид
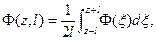 (7.42”)
(7.42”)
Истинное распределение поля находится из этого выражения путем его дифференцирования по параметру z
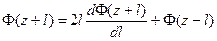 (7.43)
(7.43)
Используя разностное соотношение (7.43), можно восстановить истинное значение поля на всей оси, если известно его значение на интервале длиной 2l. В качестве исходного интервала удобно взять интервал, где соблюдается соотношение 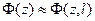 .
.
Дата добавления: 2020-08-31; просмотров: 553;











