Взаимодействия гамма-квантов с веществом

В ядерной геофизике используются только наиболее проникающие излучения — нейтроны и гамма-кванты, «просвечивающие» систему скважина-пласт через стальную обсадную колонну и цементный камень. Реакции, вызываемые нейтронами в горных породах, значи­тельно разнообразнее реакций, вызываемых гамма-квантами. Поэтому стационарные и импульсные нейтронные методы широко применяются на месторождениях неф­ти, газа и других полезных ископаемых для определения коллекторских свойств горных пород, выявления продуктивных объектов, контроля разработки месторождений, элементного анализа пород и минерального сырья, решения многих других важных задач.

Мерой взаимодействия гамма-квантов (как и других частиц) с веществом являются эффективные сечения взаимодействия – микроскопическое и макроскопическое. Микроскопическое сечение s определяет вероятность взаимодействия одной частицы с другой частицей-мишенью (ядром, электроном, атомом). Макроскопическое сечение Σ – это мера вероятности взаимодействия частицы с единицей объема вещества; оно равно произведению микросечения на число мишеней в единице объема. По исторически сложившейся традиции, макросечение для гамма-квантов обычно называют линейным коэффициентом ослабления и обозначают m (а не Σ). Величина 1/Σ определяет длину свободного пробега для конкретного типа взаимодействия.

Гамма-излучение ослабляется в веществе вследствие: фотоэффекта; комптоновского эффекта; образования пар; фотоядерных взаимодействий.

При фотоэффекте (Рис.7.1a) гамма-кванты взаимодействуют с электронной оболочкой атома. Возникающий фотоэлектрон уносит часть энергии гамма-излучения Е=hv-E₀, где E₀ – энергия связи электрона в атоме. Процесс идет при энергиях не более 0,5 МэВ. В результате фотоэффекта также возникает характеристическое рентгеновское излучение.

Микроскопическое сечение фотоэффекта зависит от энергии гамма-кванта и порядкового номера Z элемента

s_ф=12,1 Е^–3,15 Z^4,6 [барн/атом].

Сильная зависимость от Z позволяет использовать фотоэффект для количественного определения содержаний тяжелых элементов в горных породах (рентген-радиометрический и селективный гамма-гамма-методы).

При комптоновском эффекте гамма-излучение взаимодействует с электронами, передавая им часть энергии, и затем распространяется в горной породе, испытывая многократное рассеяние с изменением первоначального направления движения. Этот процесс возможен при любых энергиях гамма-квантов и является основным при 0,2<Е<3 МэВ, т. е. именно в области спектра первичного излучения естественно-радиоактивных элементов.

Рис.7.1а,б. Основные типы взаимодействий гамма-излучения с веществом (а) и диапазоны энергий и атомных номеров, в которых они проявляются (б) (МАГАТЭ, 1976 г.):

1 – фотоэффект; 2 – комптоновское рассеяние; 3 – эффект образования электрон-позитронных nap

Процесс образования электрон-позитронных пар, возникающих из фотонов в поле ядер атомов, наиболее вероятен для пород, содержащих тяжелые элементы (см. Рис.7.1б) при энергиях не менее 1,02 МэВ.

Таким образом, при различных энергиях гамма-кванты взаимодействуют преимущественно с различными мишенями: атомами, электронами, атомными ядрами.

В области энергий, где наиболее существенны комптон- и фотоэффекты (Рис.7.1б), полное макроскопическое сечение взаимодействия (называемое также линейным коэффициентом ослабления)

m=m_ф+m_к=m_к (1+m_ф /m_к ) (7.1)

где m_к=n_es_к – макросечение комптон-эффекта; n_e – число электронов в единице объема.

Электронная плотность сред, состоящих из элементов с отношением Z/A=1/2, строго пропорциональна объемной плотности (такие среды называются «нормальными»). Вследствие присутствия водорода, для которого Z/A=1, горные породы отличаются от «нормальных» сред; мерой этого отличия является «коэффициент приведения к нормальной среде».

Эффективный атомный номер cреды сложного состава – это порядковый номер такой моноэлементной среды, сечение фотоэлектрического поглощения которой такое же, как в данной многоэлементной среде.

Для моноэлементной среды n_e=dN_AZ/A, где N_A – число Авогадро; А и Z – массовое число и порядковый номер; d – плотность. Элементы, входящие в состав породообразующих минералов Поскольку условие устойчивости атомных ядер (условие насыщения ядерных сил) требует, чтобы A=N+P»N+Z»2Z, (N»Z) (где N и Р – числа нейтронов и протонов в ядре), то Z/A=0,5 независимо от типа элемента (единственное исключение составляет водород).

Таким образом, при комптоновском рассеянии макросечение m_к определяется плотностью (величина 2dZ/A называется электронной плотностью). Этот факт служит строгим физическим обоснованием плотностной модификации гамма-гамма-метода (ГГМ). В энергетической области комптон-эффекта m»d, и величина

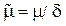(7.2)

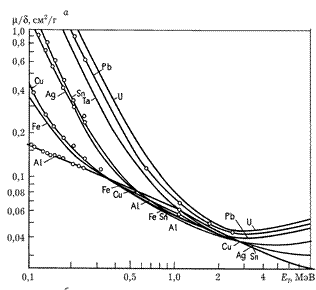
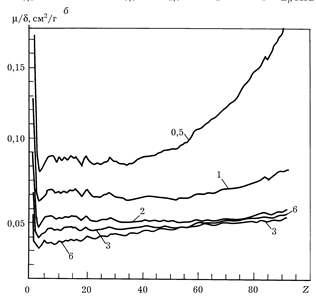
не зависит от плотности (Рис.7.2b); эта величина называется «массовым коэффициентом ослабления».

Рис.7.2а,б. Зависимости массового коэффициента ослабления m/d от энергии гамма-квантов (а) и атомного номера Z элемента (б). Шифр кри вых – энергия гамма-квантов, МэВ

Для удобства сравнения влияния фотоэффекта и комптоновского рассеяния используется сечение фотопоглощения на один электрон

s_ф/Z = P_e ×10^–2 (E/132)^–3,15 , (7.3)

где величина Р_е («индекс фотоэлектрического поглощения») равна (Z/10)^3,6. Отношение сечений m_ф/m_к=s_ф/Z_sк»P_e/s_к. Эффективный атомный номер Z_эф выражается следующим образом (для многоэлементной среды):

(7.4)

где Z_i, A_i,P_i – порядковыйномер, атомный вес и весовая(массовая) доля i-го элемента соответств 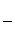енно и суммирование распространено на все элементы в естественной смеси.

Ослабление и нтенсивности dJ широкого пучка гамма-излучения в плоском слое однородного вещества толщиной dx описывается дифферен­ци­альным уравнением, аналогичным закону радиоактивного распада:

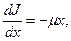
(7.5)

в интегральной форме

J(x) = J₀ exp(–mx). (7.6)

Если плотность среды зависит от x («барьерная» геометрия), то-есть μ = μ(x), то

J(x) = J₀ exp[–Λ(x)], (7.7)

где Λ – оптическая толщина слоя х, или

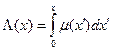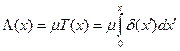, (7.8)

где Т(х) – массовая толщина слоя х; 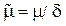- массовый коэффициент ослабления.

Для точечного изотропного источника на экспоненциальный закон ослабления (7.7) накладывается закон геометрической расходимости 1/(4pr²) в сферической геометрии («закон обратных квадратов»):

J(r) = J₀ exp(–mr)/ (4pr²). (7.9)

Это выражение описывает пространственное распределение нерассеянного (нейтронного или гамма-) излучения. Спектр многократно рассеянного излучения (Рис.7.3) от моноэнергетического источника включает рассеянное излучение, но с уменьшением энергии все больший вклад дает многократно рассеянное излучение. Пока сечение фотоэффекта мало, определяющим фактором является электронная плотность вещества, которая, в свою очередь, определяется плотностью среды. С увеличением сечения фотоэлектрического поглощения (в соответствии с уменьшением энергии гамма-квантов) амплитуда спектра убывает, и определяется уже не только плотностью, но и эффективным атомным номером вещества (индексом фотоэлектрического поглощения). Поэтому спектрометрическая регистрация позволяет определять не только плотность породы, но и ее эффективный атомный номер (литологический тип породы). Эта модификация ГГМ называется «селективной».

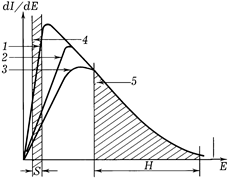Рис.7.3. Спектр многократно рассеянного гамма-излучения в породах одинаковой плотности, но различного состава (по И.Г.Дядькину, 1978 г.; В. Бертоз­зи, Д. Эллису, Дж. Волу, 1981 г.):

1-3 – атомные номера Z соответственно малые, средине и большие; 4 – область фотоэффекта и комптоновского рассеяния; 5 – область комптоновского рассеяния, S – мягкая часть спектра; H – жесткая (комптоновская) часть спектра

При селективной модификации ГГМ (ГГМ-С) применяют источники и детекторы мягкого гамма-излучения. Показания ГГМ-С зависят как от комптоновского рассеяния гамма-квантов (следовательно, от плотности среды), так и от их поглощения, которое определяется концентрацией в породе тяжелых элементов. Интерпретационный параметр метода – сечение фотоэлектрического поглощения - Р_е [барн/электрон]. Макроскопическое сечение поглощения в единице объема вещества обозначается через U, называется параметром фотопоглощения [барн/см³] и определяется выражением:

U=P_е·б_е ,

где б_е - электронная плотность. Параметр U имеет линейную петрофизическую модель. Это позволяет включать данные ГГМ-С в систему петрофизических уравнений для определения литологического состава и пористости полиминеральных отложений. Например, для двухкомпонентной модели среды (скелет и флюид, заполняющий емкостное пространство) индекс фотоэлектрического поглощения определяется выражением:

U=К_п·U_фл+(1-К_п) ·U_ск , (7.10)

где U_фл , U_ск – соответствующие параметры флюида и скелета соответственно.

Естественная радиоактивность

Естественная радиоактивность представляет собой самопроизвольный, подчиненный определенному статистическому закону распад неустойчивых ядер атомов. Радиоактивный распад приводит к изменению строения, состава и энергии ядер и сопровождается испусканием a- и b-частиц или захватом электрона из K- или L-оболочки, коротковолновым излучением электромагнитной природы (g-излучение). При этом происходят выделение радиогенного тепла, ионизация газов, жидкостей и твердых тел.

В природных условиях отмечается также спонтанное деление тяжелых ядер. Осколки деления могут образовывать треки и дефекты в кристаллической структуре минералов.

Закон радиоактивного распада естественных и искусственных радиоактивных ядер (Э. Резерфорд и Ф. Содди, 1902 г.) описывает зависимость между количеством распадающихся и имеющихся радиоактивных атомов. В дифференциальной форме он имеет вид:

dN/dt = –lN , (7.11)

где dN – число распадающихся ядер из общего количества N за время dt; l – постоянная, характеризующая скорость распада данного элемента. Величина А=lN определяет число распадов в единицу времени и называется активностью. После интегрирования получаем экспоненциальный закон изменения количества радиоактивных атомов во времени:

N(t)=N₀ exp(–lt), (7.12)