Физическая, статическая и динамическая аномалии
Физической аномалией называется область пространства (геологическое тело), отличающаяся от вмещающей среды по величине какого-то физического свойства. В геологическом разрезе аномалии физическогосвойства порождают аномалии соответствующего физического поля. Непрерывная кривая, соединяющая результаты поточечных измерений в скважине неподвижным прибором (в статике) при его последовательном перемещении по стволу скважины называется статической аномалией.
Процесс регистрации нейтронов и гамма-квантов детектором имеет статистический характер (как и сам радиоактивный распад), из-за чего статическая аномалия характеризуется наличием флюктуационной дорожки.
Регистрируемая величина – скорость счета импульсов N в единицу времени – является случайной величиной и подчиняется распределению Пуассона:
P(k)=exp(-N)Nk/k! (7.22)
Здесь N – среднее значение, Р(к) – вероятность получить при измерениях значение к. Дисперсия этого распределения σ2=N совпадает со средним. Среднеквадратическое отклонение σ=√N.
При многократной регистрации частиц в одних и тех же условиях в равные интервалы времени среднеквадратическое отклонение результатов отдельных измерений от истинного счета N составит 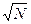 , т. е. относительная среднеквадратическая погрешность
, т. е. относительная среднеквадратическая погрешность
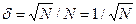 (7.23)
(7.23)
уменьшается с ростом числа N=Iτзарегистрированных частиц. Уменьшение относительной погрешности измерений достигается увеличением эффективности счетчиков, мощности источников, увеличением времени измерений (уменьшением скорости регистрации диаграмм).
Для сглаживания (осреднения) диаграммы в цепь счетчика включается интегрирующая ячейка (Рис.7.5), состоящая из емкости С и резистора R. Произведение RC = t называется «постоянной времени» ячейки. Кривая, изображающая результаты непрерывных измерений движущимся прибором, перемещающимся с равномерной скоростью по стволу скважины (в динамике) называется динамической аномалией.
При интерпретации данных радиометрии прежде всего возникает задача восстановления статической (усредненной) аномалии по динамической. Рассмотрим связь между ними.
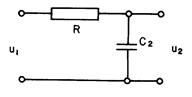
Рис. 7.5. Схема интегрирующей ячейки.
Напряжение на входе ячейки U1, определяющееся амплитудой статической аномалии J1 = dU1/dt, падает на резисторе R и емкости C; выходное напряжение U2, определяющее амплитуду динамической аномалии J2 = dU2/dt, снимается с емкости С.
В цепи интегрирующей ячейки имеем
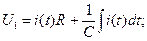 (7.24)
(7.24) 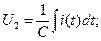 (7.25).
(7.25).
Отсюда следует
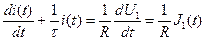 (7.26)
(7.26) 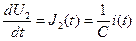 (7.27)
(7.27)
Линейное дифференциальное уравнение (3) первого порядка (типа Бернулли) имеет решение
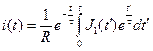 , ,
|
Откуда, на основании (7. 27) 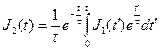 (7.28)
(7.28)
Зная скорость равномерного перемещения прибора v по стволу скважины, перейдем от времени измерений t к глубине z точки измерений z =t/v
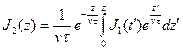 (7.29)
(7.29)
На основании (6) статическая и динамическая аномалии связаны также дифференциальным соотношением
J1 = J2(z) + vt 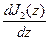 . (7.30)
. (7.30)
Для изучения статической аномалии необходимо рассчитать показания детектора против одиночного активного пласта. Для этого нужно задать функцию пространственного распределения рассеянного излучения точечного источника. Для простоты и наглядности промоделируем статическую аномалию физической. Зададим ее в виде:
ì0, z £ 0
J1 = íJ , 0 £ z £ h (7.31)
î0, z ³ h
Подставляя (7.31) в (7.29), находим:
ì0, z £ 0
J2(z) = íJ [1— exp(-z/vt)] , 0£ z £ h (7.32)
î J [1— exp(-h/vt))]exp[- ( z-h)/vt]. z ³ h
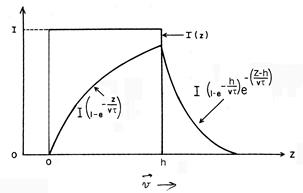
График этой функции показан на Рис.7.6.
Процессы зарядки и разрядки конденсатора искажают форму аномалии, «перетаскивают» ее в направлении движения прибора (это направление по умолчанию задается положительным направлением оси z).
Рис.7.6. Динамическая аномалия, создаваемая моделью ступенчатой статической аномалии для одиночного пласта толщиною h.
|
Для уменьшения изрезанности диаграмм и статистических ошибок увеличивают постоянную интегрирующей ячейки τ =RC, т. е. время, в течение которого усредняется скорость счета. Считают, что показания в каждой точке диаграммы соответствуют средней скорости счета в интервале времени 2τ. Поэтому статистическую ошибку показаний на диаграмме можно получить из формулы (7.23), подставив вместо N величину 2Iτ, где I — скорость счета за единицу времени. Это дает для определения относительной погрешности формулу
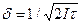 (7.33)
(7.33)
Увеличение τ приводит к уменьшению статистических флуктуации на диаграмме (к сглаживанию диаграмм); точность же замеров в среднем по пласту не увеличивается. Однако увеличение τ при данной скорости регистрации приводит также к искажению диаграмм на границе пластов, к росту переходной зоны между пластами, имеющей промежуточные показания. Поэтому от динамических аномалий необходимо переходить к статическим.
Следуя В.Н.Дахнову, рассмотрим более реалистичную модель статической аномалии, учитывающую основные закономерности поля излучения в системе скважина-пласт. Пусть необсаженная скважина диаметром 2r0 пересекает одиночный пласт толщиной h с повышенной (на фоне вмещающих отложений) радиоактивностью; скважина заполнена неактивной жидкостью, плотность которой совпадает с плотностью пласта и вмещающих отложений. Прибор расположим на оси скважины в некоторой точке М (Рис.7.7). Для простоты зададим функцию распределения точечного источника в лучевом приближении. Тогда
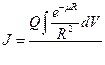 (7.34)
(7.34)
В цилиндрической системе координат (r, z) с началом в точке М
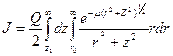
(интегрирование по азимутальному углу выполняется сразу). Выполняя подстановку
X=m (r2+z2) 
Получим (7.35)
Где Е1(x) – интегрально показательная функция:
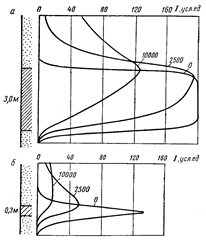
На Рис.7.7a,b показаны статические аномалии против пластов различной мощности. Эти аномалии симметричны относительно середины пластов; максимальные амплитуды Jµ аномалий для пластов достаточной большой толщины h не зависят от h (такие пласты называются «насыщенными по мощности»). Координаты границ (кровли и подошвы) пластов соответствуют половинам максимальных амплитуд для пластов. Максимум динамической аномалии всегда находится на пересечении со статической, причем сохраняется равенство площадей этих аномалий (теорема о площади аномалии):
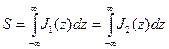 .(7.36)
.(7.36)
Это же соотношение можно представить в другом виде
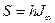 , (7.37)
, (7.37)
где – h истинная мощность пласта, 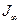 - амплитуда аномалии для пласта бесконечной мощности (так называемого «пласта, насыщенного по мощности»).
- амплитуда аномалии для пласта бесконечной мощности (так называемого «пласта, насыщенного по мощности»).
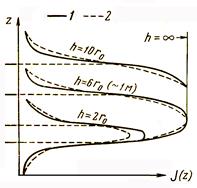 Рис.7.7a,b. Статические (а) и динамические (б) аномалии для пластов разной толщины (по В.В.Ларионову).
Рис.7.7a,b. Статические (а) и динамические (б) аномалии для пластов разной толщины (по В.В.Ларионову).
| 
|
Амплитуды статических аномалий вычисляются по динамическим на основе рекуррентного соотношения (последующие значения вычисляются через предыдущие), полученного на основе точного решения краевой задачи инерционности (А.М.Морозов). Это соотношение имеет вид
J(hi+1) = (1- ai)I(hi+1) + aiJ(hi), (7.38)
ai = exp[-(hi –hi+1)/vt], I = 1, 2, ….N-1, (7.39)
где I(hi) - амплитуда статической аномалии, не искаженной инерционностью, J(hi) - амплитуда динамической аномалии, искаженная инерционностью; hi - координата кровли или подошвы (в зависимости от направления движения прибора по стволу скважины) i -го пласта или глубина i - той точки дискретности при цифровой обработке кривой; v - скорость движения прибора (м/сек). Алгоритм восстановления статической аномалии вытекает из выражения (7.38). При постоянном (фиксированном) шаге квантования Dh имеем
ai = exp[-Dh /vt] = a, (7.39”)
и окончательно
Ii+1 =(Ji+1 - aJi)/ (1- a). (7.40)
Дата добавления: 2020-08-31; просмотров: 907;











