Погрешности представления чисел

Как уже отмечалось, представление числовой информации в цифровом автомате, как правило, влечет за собой появление погрешностей (ошибок), величина которых зависит как от формы представления чисел, так и от длины разрядной сетки цифрового автомата, т.е. компьютера. Следовательно, при переводе чисел из одной системы счисления в другую неизбежно возникают погрешности.

Абсолютная погрешность представления - это разность между истинным значением входной величины А и ее значением, полученным из машинного изображения Ам, т.е.

[A] = A - Aм

Тогда относительная погрешность представленияравна:

[A] = [A]/Av

Максимальная погрешность перевода десятичной информации в двоичную не превышает единицы младшего разряда разрядной сетки цифрового автомата. Минимальная погрешность перевода равна нулю.

Усредненная абсолютная погрешность перевода чисел в двоичную систему счисления будет равна:

[A]c = 0,52-n для дробей и

[A]c= 0,520 для целых чисел

Для представления чисел в форме с фиксированной запятой абсолютное значение машинного изображения числа лежит в пределах:

2-n [A]ф 1 - 2-n для дробей и

20 [A]ф 2n- 1 для целых чисел

Следовательно, относительные погрешности представления для ми-нимального значения числа равны:

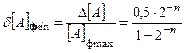для дробей и

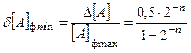для целых чисел.

Аналогично для максимального значения:

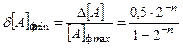для дробей и

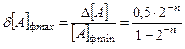для целых чисел.

Как видим погрешности представления малых чисел в форме с фиксированной запятой могут быть очень значительными.

Для представления чисел в форме с плавающей запятой абсолютное значение мантиссы лежит в пределах

2-1 |[mA]n| 1 - 2-n.

Так как погрешность представления числа зависит только от разрядности мантиссы, то для нахождения погрешности представления числа в форме с плавающей запятой величину этой погрешности надо умножить на величину порядка числа p:

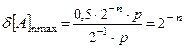
и

=

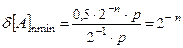где n - количество разрядов для представления мантиссы числа. Из последней формулы следует, что относительная точность представления чисел в форме с плавающей запятой почти не зависит от величины числа.

Глава 4.