Форма представление чисел с плавающей запятой

В общем случае число в форме с плавающей запятой представляется в виде:

A = mq p ,

где m - мантисса числа, q - основание системы счисления, q p - порядок числа, который для упрощения в примерах будем иногда изображать как P. Тогда очевидно, что p - это показатель степени порядка, который обычно называют просто порядком числа, т.к. в основном всегда q = 2. Следовательно предыдущее выражение можно записать в следующем виде:

A = mAPA,

имея в виду, что в компьютерах обычно q = 2.

Так, например, число 1984 в форме с плавающей запятой в десятичной системе счисления можно записать следующим образом:

1984,0100 0,1984104

19,84102 19840010-2

и т.д.

Число с плавающей запятой принято представлять в так называемом нормализованном виде для максимально точного представления числа. Если выполняется неравенство

q-1 |m| <1,

а в случае двоичной системы счисления:

0.5 |m| <1,

то считается, что число представлено в нормализованном виде. Например, 0,1984104 является нормализованным видом числа 1984 в форме с плавающей запятой в десятичной системе счисления.

Таким образом, у двоичного нормализованного числа в форме с плавающей запятой мантисса - правильная дробь и в старшем разряде мантиссы всегда стоит 1. Операция приведения числа к нормализованному виду называется нормализацией. Нормализация чисел в компьютере выполняется или автоматически или же по специальной программе.

Так как система счисления для заданного цифрового автомата (ком-пьютера) остается постоянной, то при представлении числа в формате с плавающей запятой нет необходимости указывать ее основание, достаточно лишь представить показатель степени порядка числа.

Для представления двоичного числа в форме с плавающей запятой в разрядной сетке, выделенной для этой цели, отводится по одному разряду для представления знака числа Smи знака показателя степени порядка SP; определенное число разрядов для представления значения самого показателя p, а также разряды для размещения значения модуля мантиссы m. Например, возможен следующий вариант:

Sp p Sm m

т.е.

[A] = Sp pASmmA

Обычно в формате с плавающей запятой вместо показателя p используют так называемую характеристику ("смещенный порядок"):

r = p + l,

где l - избыток (смещение), значение которого подбирается таким образом, чтобы при изменении значения показателя от некоторого минимального значения -|pmax| до максимального +|pmax|, характеристика r менялась от 0 до rmax. Следовательно, характеристика не меняет своего знака. В таком случае отпадает необходимость в отображении знака порядка Sp. Для этого принимается, что

l = 2k-1,

где k - число разрядов, выделеных для представления порядка числа в формате с плавающей запятой.

Тогда формат числа с плавающей запятой можно представить, в частности, следующим образом:

Sm r m

т.е.

[A] = Sm r mA

Такой формат и используется, в основном, в настоящее время.

Рассмотрим несколько примеров представления чисел в форме с плавающей запятой. Предварительно напомним, что показатель степени двойки в разрядах разрядной сетки длиной n, отведенной для представления целых чисел, изменяется от 0 до n-1, а в случае правильных дробных чисел - от -1 до -n.

Если для представления показателя порядка выделены 4 разряда, то

l = 23= 810= 10002. Для этого случая в таблице 3.1 приведены значения показателя порядка, характеристики и мантиссы для некоторых чисел, представленных в форме с плавающей запятой.

Т а б л и ц а 3.1.

A10 p10 r10 m2

0 0 8 0,0

1 1 9 0,1

2 2 10 0,1

3 2 10 0,11

0,5 0 8 0,1

0,25 -1 7 0,1

0,75 0 8 0,11

0,375 -1 7 0,11

Например, в 16-ти разрядных компьютерах для представления двоичного числа в форме с плавающей запятой с обычной точностью отводится 4 байта, т.е. 2 16-разрядных слова:

15 14 7 6 0 старшее

1$0 r старшая часть |m| слово

15 0 младшее

младшая часть |m| слово

Разряды 147 старшего слова числа используются для представления характеристики числа. В остальных разрядах старшего слова и во всем младшем слове размещается модуль мантиссы числа. 15-й разряд старшего слова используется под знак числа.

Единица самого старшего разряда нормализованной мантиссы обычно является "скрытой", т.е подразумевается и не отражается в формате числа.

7-ой разряд старшего слова, в котором должна была быть отражена эта единица, используется в качестве младшего разряда характеристики, что позволяет увеличить диапазон представления чисел в формате с плавающей запятой.

Таким образом, мантисса в таком варианте отображается, начиная с разряда, следующего после самого старшего. При всех операциях с мантиссой числа это обстоятельство надо учитывать и перед началом этих операций восстанавливать старший разряд мантиссы в тех регистрах, куда загружается мантисса числа для выполнения над ней каких-то процедур.

После завершения этих процедур во время формирования отображения нормализованного числа в отведенной для него разрядной сетке машинных слов, старшая единица мантиссы опять отбрасывается.

8-разрядное поле порядка позволяет изменять показатель порядка в пределах от -12810 до +12710, причем показатель порядка записыватся с избытком l = 2008 или 12810.

В отличие от показателя порядка, как уже отмечалось, характеристика не меняет своего знака и в данном случае изменяется от 0 (при p = -12810) до 3778 (при p = +12710), причем r = 2008 при p = 0. Исключение составляет число 0: ноль с обычной и двойной точностью выражается нулевой характеристикой и нулевой мантиссой.

Примеры представления чисел в форме с плавающей запятой в

16-разрядных компьютерах приведены в таблице 3.2:

Т а б л и ц а 3.2.

A10 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 A8

1 1 1 040200

2 1 1 040400

7 1 1 1 1 1 040740

10 1 1 1 041040

0,5 1 040000

0,25 1 1 1 1 1 1 1 037600

-2 1 1 1 140400

-7 1 1 1 1 1 1 140740

0 000000

А8 - представление старшего слова числа в форме с плавающей запятой в восьмеричном коде.

Во всех приведенных примерах содержимое младшего слова числа равно нулю. В случае представления числа с плавающей запятой с двойной точностью, под мантиссу отводится еще два 16-ти разрядных слова, т.е. для представления числа в такой форме отводится 4 16-ти разрядных слова.

Например, в микропроцессоре 80386 предусмотренно три варианта представления числа ("действительного" числа) в форме с плавающей запятой: с разрядностью 32, 64 и 80 бит. В первом случае под характеристику выделяется 7 разрядов, а в остальных - по 8.

Длина разрядной сетки, выделенной под характеристику, определяет диапазон представления чисел в формате с плавающей запятой.

Как уже отмечалось, модуль мантиссы нормализованного числа - mА, представленного в формате с плавающей запятой лежит в пределах:

2-1 mА (1 - 2-n)

где n - число разрядов, выделенных для представления мантиссы числа А. Если для представления порядка (p) выделено k разрядов, то

pmin= -2k b pmax= (2k-1)

Тогда диапазон, в котором может быть представлено число в формате с плавающей запятой, будет равен:

2Pmin2-1 A (1 - 2-n)2Pmax

или

.

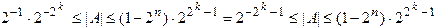Основным преимуществом представления чисел в форме с плавающей запятой является большой диапазон машинных чисел и высокая точность их представления. Диапазон определяется длиной разрядной сетки, выделенной под характеристику, а точность - определяется длиной разрядной сетки, выделенной под мантиссу.