Параметрические кубические поверхности Форма Эрмита.

Параметрические кубические поверхности Форма Эрмита

поверхности задаются кубическими уравнениями от 2-х переменных – s и t.

0<=s/t<=1

X(s,t)=a11s3t3+a12s3t2+a13s3t+a14s3+a21s2t3+a22s2t2+a23s2t+a24s2+a31st3+a32st2+a33st+a34s+a41t3+a42t2+a43t+a44.

X(s,t)=sCxTT ; s=(s3,s2,s,1); T=(t3,t2,t,1)

Форма Эрмита-

x(s)=SMhGhx

X(s,t)=SMhGhx(t)=SMh*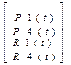

P1x(t), P4x(t) – описывают начальную и конечную точки кривой, задаваемой параметром S.

Для каждого t определяются 2 конечные точки. R1x(t) R4x(t) описывают начальные и конечные касательные векторы к точкам кубической кривой, построенных в зависимости от параметра S.

Путем несложных преобразований получим: x(s,t)=SMhQxMntTT. Определим Qx

Qx=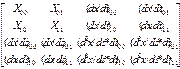

Где x – координаты конечных точек кривой, 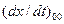- тангенсы углов наклонов координат, 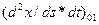- кривизна.

Форма Безье

X(s,t) = SMbPXMbTTT

Форма В-сплайнов

X(s,t) = SMSPXMSTTT

38. Методы создания реалистических изображений

Неопределённость восприятия

Нужно избавится от неопределённости

Методы удаления неопределённости

1) удаление скрытых поверхностей и линий

2) закраска видных поверхностей, освещение

3)текстурирование

1) основной трудностью создания реалистичного изображения является сложность реальных визуальных объектов

2) основная цель создания реалистичных изображений состоит в том при выводе на дисплей дать достаточно информации пользователю. Чтобы он однозначно понимал трёхмерные пространственные отношения между объектами.

3) 3-х мерные объекты приходится проецировать на плоскость

4) проецирование приводит к существенным потерям инфы а иногда и к неопределённости изображения

5) в перспективной проекции не теряется информация о глубине

6)размеры объекта обратно пропорциональны расстоянию от наблюдателя

7) вид объекта зависит от освещения

8)текстуры формируют фактуру объекта тем самым улучшая его идентификацию

Чем больше у пользователя информации об объекте тем он скорее сформирует для себя гипотезу объекта и хотя гипотеза формеруется и на самых примитивных уровнях представления, конечная цель его реалистичность.

39. Удаление скрытых линий (HSR). Тезисы

Алгоритм удаления скрытых линий делится на 2 класса

1) Алгоритм отсечения в пространстве изображения

2) Алгоритм отсечения в пространстве объекта

Для первого класса объект рассматривается как совокупность

n угольных граней и необходимо определить какая грань видна в каждой точке разрешения экрана

кол-во операций N*K

где К – кол-во точек на экране.

для второго класс каждая из граней n сравнивается с остальными n-1 гранями

число операций n^2

Правила:

1) удаление должно проводиться в трёхмерном пространстве

2) сравнение по глубине сводим к выяснению закрывает ли одна из заданных точек другую, лежат ли точки на одном и том же проекторе (линия проецирования)

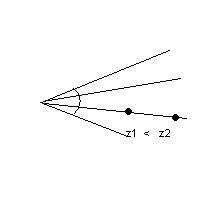
Ортографическая проекция х1 = х2, у1 = у2, z1 = z2

Перспективное проецирование x1/z1 = x2/z2, y1/z1 = y2/z2

Для упрощения алгоритмов можно пользоваться свойством выпуклости их оболочек.

Сначала смотрим пересекаются ли оболочки а потом смотрим на объекты.