НЕПАЛИТРОВЫЕ РЕЖИМЫ АДАПТЕРОВ SVGA

Ряд SVGA-карт поддерживает использование так называемых напалитровых режимов - для каждого пиксела вместо индекса в палитре непосредственно задается его RGB значение. Обычно такими режимами являются режимы HiColor (15 или 16 бит на пиксел) и true color (24 бита на пиксел).

Видеопамять устроена аналогично 256-цветным режимам SVGA - под каждый пиксел отводится целое количество байт памяти (2 байта для HiColor и 3 байта для TrueColor), и все они расположены подряд и сгруппированы в банки.

Наиболее простой является организация режима TrueColor - под каждую из трех компонент цвета отводится по одному байту.

Несколько сложнее организация режимов HiColor, где под каждый пиксел отводится 2 байта и возможны варианты:

под каждую компоненту отводится по 5 бит, последний бит не используется (32 тысячи цветов)

под красную и синюю компоненты отводится по 5 бит, под зеленую - 6 бит (64 тысячи цветов).

30. Аппаратные ускорители графики. 3D-конвейер.

Видеоконтроллер с потоковой обработкой а также с аппаратной поддержкой некоторых типовых функций называется ускорителем (акселератором) и служит для разгрузки ЦП от рутинных операций по формированию изображения.

D – конвейер.

1) Определение состояния объектов (Situation modeling)

2) Определение соответствующих текущему состоянию геометрических моделей

(Geometry generation).

3) Разбиение геометрических моделей на примитивы(Tesselation). Это первая стадия конвейера которая аппаратно зависима. Самый распространенный примитив треугольник.

4) Привязка текстур освещения (Texture and Light definition).Высчитывается только для вершин.

5) Видовые геометрические преобразования (Projection). Определяет координаты мира относительно пользователя. трансформируется из 3D в 2D, то есть проецируется.

6) Отбрасывание не видимых примитивов (Culling).На этом этапе удаляются вершины и примитивы которые полностью невидимые

7) Установка примитивов (Setup). Инф. о примитивах (коор, вершины, наложение текстур, освещение) преобразуются в вид пригодный для последующей стадии(преобр, в целые числа фиксированного размера которые понимает аппаратура)

8) Закраска примитивов (Fill).Формируется растр.

9) Финальная обработка (Post processing).

Некоторые стадии конвейера могут быть переставлены местами, разбиты на части или совмещены. Они могут отсутствовать вообще(редко) или могут появляться принципиально новые (часто). Результат любой стадии конвейера может быть отослан обратно в обход других стадий.

31. Аппаратная структура ускорителя. Ускорители будущего.

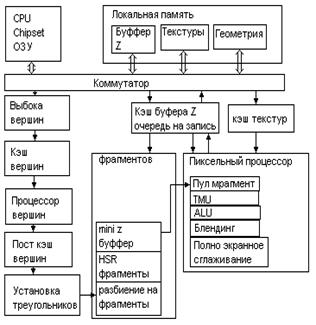
Важное отличие граф. Ускорителей от процессора то что потоковый и предсказуемый характер данных позволяет обходится небольшим кэшем высокой эффективности. На логическом уровне длина конвейера более 100 стадий что приводит к невозможности использования процессоров высокой тактовой частоты.

Аппаратная графическая под система будущего.

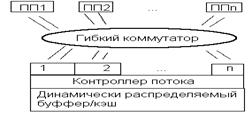
Хар-ки:

1.Динамическое распределение ресурсов.

2.Большой массив одинаковых по возможностям процессоров.

3.Общий коммутатор.

4.Большой набор контроллеров очередей и доступов к памяти.

5.Только цифровые интерфейсы все на основе массива последовательных шин общего назначения.

6.Память работающая на прямую с такими шинами.

7.Устройство вывода с общими периферийными интерфейсами.

8.Фокусировка на качестве.

9.Стерео дисплеи.

Определение объектов:

32. Представление пространственных форм. Полигональные сетки.(км)

В общем случае объект не может в точности соответствовать реальному.

Уровень подобия

Объект можно представить каким-то уровнем подобия с помощью математических формул

Автоматизированное представление

Автоматизированное проектирование

Нет заранее известной модели

В данной главе введение в область геометрического моделирования

Конструирование форм

1) Полигональные сетки

2) Бикубические поверхности

Полигональные сетки -совокупность рёбер вершин и многоугольников, вершины соединены рёбрами, а многоугольники последовательностью ребер

Оценки представлений полигональных сетей

1) Объём требуемой памяти

2) Простота:

1) Идентификации рёбер

Инцидентных вершин

2) Идентификации многоугольников, которым принадлежит данное ребро

3) Процедура поиска вершин

Обр. ребра

4) Определение рёбер образующих многоугольник

5) Получение изображения полигональной сетки

6) Обнаружение ошибок в представлении

33. Формы задания: явная, указатели в список вершин, явное задание ребер

1) Явное задание многоугольников

Р= список координат вершин

Р=((x1,y1,z1),…,(xn, yn,zn))

А) вершина А дублируется

Б) задача поиска многоугольников имеющих общую вершину. Для этого необходимо N*log (z*N) операций.

В) При прорисовке многоугольников некоторые рёбра рисуются по несколько раз

2) Задание многоугольников при помощи указателей в список вершин

V=((x1,y1,z1), … , (xn,yn,zn)) список вершин

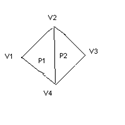
Вершины при прорисовке не дублируются

Р1=(1,2,4)

Р2=(4,2,3)

Память экономится на общих вершинах, от изменения координат вершин полигональная сетка не искажается.

По-прежнему трудно отыскивать общие рёбра и их двойные пририсовки

3) Явное задание рёбер

Имеется список вершин V

Но многоугольник не как указатель списка вершин, а как указатель на список рёбер

V=((x1,y1,z1), … , (xn,yn,zn)) список вершин

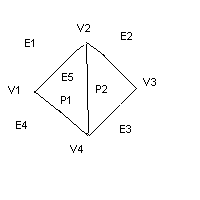
V=(V1,V2,V3,V4)

//список ребер

E1=(V1,V2,P1, R)

Е2=(V2,V3,P2,R)

E3=(V3,V4,P2,R)

E4=(V4,V1,P1,R)

E5=(V4,V2,P1,P2)

P1=(E1,E4,E5)

P2=(E2,E3,E5)

Все рёбра прорисованы по разу, можно отобразить структуру.

Недостаток – требует много памяти

34. Параметрические кубические кривые.(км)

2 вида представления кривых

1) x,y,z явное задание

2) t при помощи параметра

x=x

y=f(x)

z=g(x)

tg угла наклона может оказаться равным бесконечности

невозможно определить задаёт ли кривая петлю между 2-мя заданными точками

вместо tg в параметрическом задании используется векторы, которые не бывают бесконечными.

Опр. Параметрической кубической кривой является кривая, в которой x y z многочлены

Т.к. мы рассматриваем конечные отрезки кривой можно ограничить t в конечном диапазоне 0<=t<=1

x(t)=ax * t^3 + bx * t^2 + cx * t + dx

y(t)=ay… dy 0<=t<=1

z(t)=az… dz (2)

полное представление парам. куб кривых

dx/dt =3 * axt^2 + 2bx * t + cx (3)

задаём касательный вектор

dy/dx= (dy/dt)/(dx/dt)

dx/dz=(dx/dt)/(dz/dt) (4)

углы наклона не зависят от длинны кас вектора

если функция, задающая кривую и ее первая производная непрерывна, то 2 кривые плавно сочленяются в точках

Форма Эрмита

x(t)=T*Cx=T*Mh*Ghx аналогично:

y(t)=T*Cy=T*Mh*Ghy

z(t)=T*Cz=T*Mh*Ghz

В общем виде: P(t)=T*Mh*Gh – эрмитово представление трехмерной кубической кривой.

T*Mh=((2t3-3t2+1)(-2t2+3t2)(t3-2t2+1)(t3-t2))

X(t)= T*Mh*Ghx=P1x(2t3-3t2+1)+P2x(-2t2+3t2)+P3x(t3-2t2+1)+P4x(t3-t2)

Четыре функции переменной t в произведении T*Mh часто называют функциями сопряжения т.к. с помощью первых двух функций сопрягаются точки Р1 и Р4, а посредством других – векторы R1 и R4 в результате чего получается сглаженное объединение x(t)

36. Форма Безье. Форма В-сплайнов.

Координаты векторов определяются через точки

R1 = 3(P2 - P1 ) = P’(0)

R4 = 3(P4 - P3 ) = P’(1)

Матрица связи форм Эрмита и Безье-

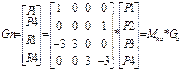
X(t)= T*Mh*Ghx = T*Mh* Mhb*Gbx = T*Mb*Gbx

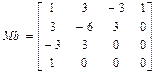
Форма Безье используется в машинной графике чаще, чем Эрмитова форма – геометрические матрицы интуитивно привлекательней в интерактивном режиме т.к. перемещая точки можно привести кривую в любую желаемую кривую. Четыре управляющие точки определяют многоугольник – выпуклую оболочку, внутри которой находится кривая Безье.

Форма В-сплайнов.

Кривая, представленная в виде кубического в-сплайна в общем случае может проходить через любые управляющие точки. Она непрерывна, также непрерывны ее касательные векторы и кривизна. Можно утверждать что кривая в-сплайна более гладкая чем другие кривые.

X(t)=T*Ms*Gsx

Ms=(1/6)*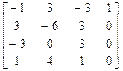

При аппроксимации управляющих точек Р1….Рn последовательностью в-сплайнов мы будем применять между каждой парой соседних точек геометрические матрицы.

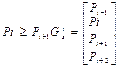2≤ i ≤n-2