Выбор экономичного режима совместной работы энергооборудования при постоянной нагрузке

При параллельной работе однородного энергетического оборудования возникает задача экономичного распределения нагрузки между работающими агрегатами. Это обеспечивает экономию народнохозяйственных затрат и, прежде всего, экономию топлива.

Наиболее просто задача может быть решена, если оборудование работает на одинаковой первичной (подведенной) мощности, получаемой из общего источника, а все агрегаты покрывают общую, постоянную для них нагрузку. Критерием экономичности работы оборудования в этом случае будет минимум суммарного расхода подведенной мощности N_аSили, что то же самое, минимум суммарных потерь N_иS, при условии покрытия заданной постоянной нагрузки N_еS = const.

Математически это формулируется следующим образом. Найти минимуму функции

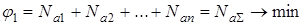(7.1)

или

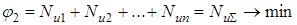(7.2)

при условии

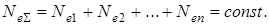(7.3)

Условие (7.3) можно переписать в виде

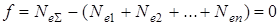(7.4)

Воспользовавшись методом Лагранжа для отыскания относительных экстремумов функции, имеющих ограничение в форме равенства, определим минимум вспомогательной функции вида

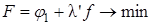(7.5)

или

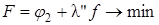, (7.6)

где l' (или l" ) – постоянный множитель.

В задачах (7.5) и (7.6) имеем n неизвестных мощностей N_еi и одно неизвестное l. Необходимым условием для получения экстремума выражения (7.5) или (7.6) (одновременно соответствующего экстремуму выражения (7.1) или (7.2)) является равенство нулю первых частных производных вспомогательной функции (7.5) или (7.6). Например,

,

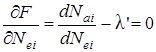откуда

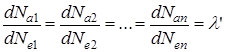
или

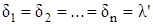(7.7)

Таким образом, для обеспечения экстремального значения функций (7.1) и (7.2) все агрегаты должны работать с мощностями, соответствующими одинаковым значениям частичных удельных расходов, равных постоянной величине l, в свою очередь зависящей от .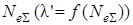

Учитывая взаимосвязь частичных удельных показателей, например, d = 1 + e, можно от условия (7.7) перейти к условию (7.8), соответствующему экстремуму функций (7.2) и (7.6).

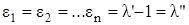, (7.8)

Однако для получения минимума суммарной подведенной мощности или потерь соблюдение условия (7.7) или (7.8) хотя и необходимо, но еще недостаточно. Чтобы эти условия соответствовали минимуму оптимизируемой функции, необходимо, чтобы энергетические характеристики оборудования были обращены выпуклостью к оси абсцисс, т. е. были вогнутыми. Такую форму имеют энергетические характеристики котлоагрегатов, гидроагрегатов, трансформаторов и линий электропередач. Для турбоагрегатов, энергетические характеристики которых линейны или обращены выпуклостью в сторону оси ординат (выпуклые), экономический режима выбирается по правилам, изложенным ниже.

Для турбоагрегатов с низкими начальными параметрами пара, имеющими энергетические характеристики выпуклой формы, соблюдение условий (7.7) и (7.8) будет – приводить не к минимуму, а к максимуму суммарной подведенной мощности или потерь. Для агрегатов с линейными характеристиками условия (7.7) и (7.8) неприменимы, поскольку отсутствуют точки с одинаковыми значениями частичных удельных показателей в связи со ступенчатым характером зависимости d = f (N). Можно показать, что экономический режим совместной работы оборудования с выпуклыми или линейными энергетическими характеристиками, обеспечивающий минимум расхода суммарной подведенной мощности или потерь, достигается последовательной догрузкой работающих агрегатов до полной мощности в порядке ухудшения их частичных удельных показателей при номинальной мощности.

Суммарная нагрузка энергетического оборудования N_еS не остается постоянной, в связи с этим состав работающего оборудования и их энергетические характеристики в отдельные моменты времени могут изменяться. Выбор оптимального состава работающего оборудования предшествует выбору экономичного режима совместной работы этого оборудования.

Построение энергетической характеристики группы совместно работающего оборудования осуществляется на основе энергетических характеристик отдельных агрегатов с учетом полученного условия экономичности совместно работающего оборудования. Наиболее просто энергетические характеристики групп оборудования получаются для однотипных агрегатов исходя из следующих простых зависимостей: N_аS = N_а × n, N_еS = N_е × n, N_иS = N_и × n, где n – число агрегатов в группе, N_е, N_а и N_и – соответственно полезная мощность, подведенная мощность и потери отдельного агрегата. Более громоздко получение энергетических характеристик групп, состоящих из оборудования с различными энергетическими характеристиками.

При выборе состава работающих агрегатов практически могут встретиться два случая (рис. 7.1):

1) энергетические характеристики различных групп агрегатов не пересекаются;

2) энергетические характеристики различных групп агрегатов пересекаются.

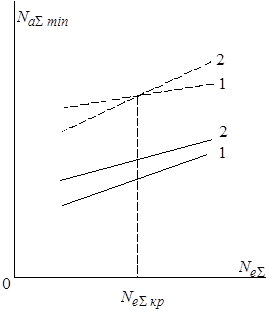
Рис 7.1. Энергетические характеристики групп совместно работающего оборудования, не пересекающиеся (сплошные линии) и пересекающиеся (штриховые линии)

В первом случае сочетание оборудования, энергетическая характеристика которого лежит ниже, будет экономичнее других при всех технически возможных для него нагрузках. Во втором случае до точки пересечения энергетических характеристик групп, более экономична одна группа, а после - другая группа, энергетическая характеристика которой проходит ниже. Таким образом, для обеспечения максимальной экономичности совместной работы энергетического оборудования при постоянной нагрузке всегда необходимо вести работу на тех группах агрегатов, энергетическая характеристика которых лежит ниже остальных.