Классический метод расчета переходных процессов

Переходные процессы в любой электрической цепи можно описать систе­мой дифференциальных уравнений, составленных для схемы цепи по законам Кирхгофа. В математике известно несколько методов решения систем диффе­ренциальных уравнений: классический, операционный, численный и др. Назва­ние метода расчета переходных процессов адекватно названию математиче­ского метода решения системы дифференциальных уравнений, которыми опи­сывается переходные процессы.

Исключая из системы дифференциальных уравнений Кирхгофа лишние переменные, получим в результате для искомой функции x(t) неоднородное дифференциальное уравнение n-го порядка:

,

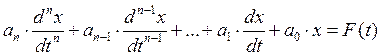где х – искомая величина, например i или u; a_k – постоянные коэффициенты; F(t) – некоторая функция времени, определяемая источником энергии.

Из курса математики известно, что решение (общий интеграл) линейного неоднородного дифференциального уравнения состоит из суммы двух решений: а) 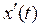- полного решения однородного (без правой части) дифференциального уравнения и б) 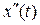- частного решения неоднородного дифференциального уравнения для t= ∞ :

.

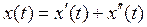Вид частного решения 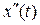для t = ∞ определяется источниками энергии и соответствует значению искомой функции в установившемся послекоммута­ционном режиме: 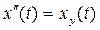. В электротехнике эта составляющая решения получила название установившейся.

Полное решение однородного дифференциального уравнения имеет вид:

,

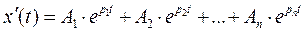где А₁, А₂,…, Аn – постоянные интегрирования; p₁, p₂,…, p_n – корни характери­стического уравнения, которое получают из однородного дифференциального, заменив в нем х→1, dx/dt→p и т.д.:

.

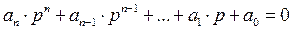Эта составляющая решения не зависит от источников энергии, в электро­технике она получила название свободной: .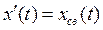

Таким образом, решение для искомой функции (тока, напряжения) может быть представлено в принятой в электротехнике форме:

.

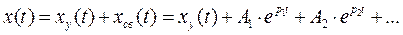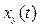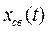Физический смысл имеет только полное решение для искомой функции x(t), а ее отдельные составляющие и являются расчетными величи­нами.

Метод расчета переходного процесса, заключающийся в решении неодно­родного дифференциального уравнения классическим методом математики, по­лучил название классического.

Расчет переходного процесса классическим методом состоит из следую­щих составных частей или этапов:

а) расчет установившейся составляющей ;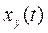

б) составление характеристического уравнения и определение его корней p₁,…, p_n;

в) определение постоянных интегрирования А₁, А₂,….

Следует отметить, что расчет переходного процесса классическим мето­дом выполняется не в строгом соответствии с математическим методом реше­ния неоднородного дифференциального уравнения. Физические законы элек­тротехники позволяют существенно упростить это решение.

5. Определение установившейся составляющей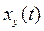

Как известно, установившаяся составляющая искомой функции 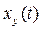, яв­ляясь частным решением неоднородного дифференциального уравнения при t=∞, соответствует значению искомой функции в установившемся после комму­тации режиме. Определение этой составляющей математическим методом из решения дифференциального уравнения довольно сложно и трудоемко. Гораздо проще найти эту функцию инженерным методом путем расчета схемы цепи в установившемся режиме после коммутации, что и делают на практике.

Пример. Определить установившуюся составляющую для тока i_у в схеме рис. 130 при заданных значениях параметров элементов: R₁=50 Ом, L=100 мГн, R₂=100 Ом, C=50мкФ, а)для постоянной ЭДС e(t)=E=150 В = const; б)для сину­соидальной ЭДС e(t)=150sinωt, f=50 Гц.

После коммутации ветвь с резистором R₂ отключается и не оказывает влияния на режим остальной схемы.

а) При постоянной ЭДС источника e(t)=Е=const ток в схеме протекать не может (сопротивление конденсатора постоянному току равно ∞), следовательно i_у(t)=0.

б) При переменной ЭДС источника e(t)=Е_msinωt расчет установившегося режима выполняется в комплексной форме для комплексных амплитуд функ­ций. По закону Ома:

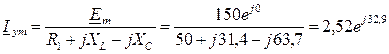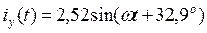A

A

Вид установившейся составляющей соответствует виду источников энер­гии, которые действуют в схеме цепи.