Движение газов по каналам переменного сечения

Рассмотрим идеальный газ, движущийся прямолинейно по каналу (трубопроводу) переменного сечения без отвода и подвода теплоты .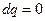

Запишем дифференциальное уравнение Эйлера вдоль оси 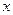, учитывая, незначительность массовых сил, и считая движение стационарным

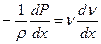( 11.11)

Массовый расход жидкости по каналу или уравнение сплошности составит:

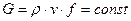
Логарифмируя уравнение сплошности

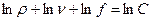
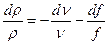
преобразуем (11.11) к виду

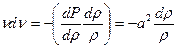
получим:

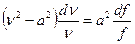, ( 11.12)

Разделим обе части (11.12) на 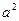, получим уравнение Гюгонио

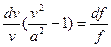( 11.13)

Отношение 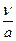представляет собой основной параметр движения газа и называется числом Маха (Маиевского) -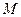

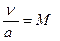(число Маха) ( 11.14)

Критерий Маха указывает на сверхзвуковые и дозвуковые течения.

Если число Маха 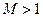, то течение газа сверхзвуковое, если 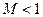, то течение газа дозвуковое

Перепишем уравнение Гюгонио в виде:

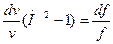(11.15)

Проведен анализ уравнения (1.15) для случаев истечения газа из сопла (плавно сужающегося насадка) и диффузора ( плавно расширяющегося насадка)

- Дозвуковое течение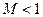

а) истечение газа из сопла т.е. 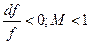, тогда 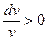т.е сужающееся сопло при дозвуковом режиме течения приводит к увеличению скорости;

б) истечение газа из диффузора т.е. 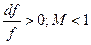, тогда 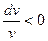. т.е при дозвуковом режиме течения, расширяющийся диффузор приводит к уменьшению скорости.

- Сверхзвуковое течение ;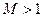

а) жидкость истекает из сопла, т.е. 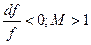, тогда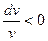

При сверхзвуковых истечениях сужающееся сопло ведет к падению скорости.

б) жидкость истекает из диффузора, т.е. 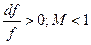, тогда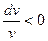

При сверхзвуковых истечениях диффузор ведет к увеличению скорости. Таким образом, в зависимости от числа Маха, сопло и диффузор могут либо увеличивать, либо уменьшать скорость истечения газа из них.

Гипотеза Сен-Венана.

Рассмотрим истечение газа из большого резервуара через суживающееся сопло в пространство (рис. 11.1). Будем считать, что газ в резервуаре неподвижен, т.е. его параметры равны параметром торможения. Давление в среде, куда происходит истечение - 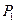, соответственно все параметры среды будут обозначаться с тем же индексом. Запишем уравнение Бернулли.

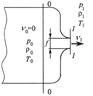
Рис. 11.1 Истечение жидкости из резервуара

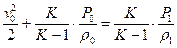( 11.16)

Из уравнения ( 11.16) выразим скорость истечения

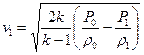( 11.17)

Учитывая, что 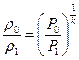, получи формулу истечения Сен- Венана.

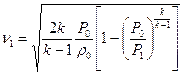(11.18)

Для того, чтобы происходило истечение жидкости из сопла в камеру, необходимо, чтобы существовало разность давлений газа в камере и в резервуаре. Начнем понижать давление 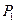, газ приходит в движение, его скорость не превышает скорости звука 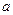. При дальнейшем снижении давления в камере, может наступить момент, когда скорость истечения в сопле достигнет скорости звука 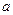. В этом случае, упругие колебания среды начнут распространяться в противоположном направлении движущегося газа, т.е. происходит так называемое, запирание движения. Скорость истечения при этом будет постоянной и равной скорости звука 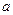. Таким образом, при изменении внешнего давления не возможно получить скорость больше скорости звука, эта гипотеза носит название гипотезы Сен-Венана.

Рост скорости газа сверх звуковых значений возможно только в комбинированном сопле Лаваля состоящего из двух частей: сужающегося и расширяющегося.