Методы Шеннона-фано и Хаффмена
В качестве примера, поясняющего принципы сжатия, рассмотрим простой метод Шеннона-Фано. В чистом виде в современных СПД он не применяется, однако позволяет проиллюстрировать принципы, заложенные в более сложных и эффективных методах. Согласно методу Шеннона-Фано для каждого символа формируется битовый код, причем символы с различными частотами появления имеют коды разной длины. Чем меньше частота появления символов в файле, тем больше размер его битового кода. Соответственно, чаще появляющийся символ имеет меньший размер кода.
Код строится следующим образом: все символы, встречающиеся в файле выписывают в таблицу в порядке убывания частот их появления. Затем их разделяют на две группы так, чтобы в каждой из них были примерно равные суммы частот символов. Первые биты кодов всех символов одной половины устанавливаются в "О", а второй — в "I". После этого каждую группу делят еще раз пополам и так до тех пор, пока в каждой группе не останется по одному символу. Допустим, файл состоит из некоторой символьной строки aaaaaaaaaabbbbbbbbccccccdddddeeeefff, тогда каждый символ этой строки можно закодировать как показано в табл. 8.1.
Таблица 8.1. Пример построения кода Шеннона-Фано
| Символ | Частота появления | Код |
| а | ||
| b | ||
| с | ||
| d | ||
| е | ||
| f |
Итак, если обычно каждый символ кодировался 7—8 битами, то теперь требуется максимум 3 бита.
Однако, показанный способ Шеннона-Фано не всегда приводит к построению однозначного кода. Хотя в верхней подгруппе средняя вероятность символа больше (и, следовательно, коды должны быть короче), возможны ситуации, при которых программа сделает длиннее коды некоторых символов из верхних подгрупп, а не коды символов из -нижних подгрупп. Действительно, разделяя множество символов на подгруппы, можно сделать большей по вероятности как верхнюю, так и нижнюю подгруппы. В качестве примера такой ситуации служат приведенные ниже две таблицы, где одни и те же символы с одинаковыми вероятностями появления в файле имеют различную кодировку.
Более удачен в данном отношении метод Хаффмена. Он позволяет однозначно построить код с наименьшей средней длиной, приходящейся на символ.
Таблица 8.2. Пример кодировки одних и тех же символов различными кодами
| Символ | Частота появления | Код |
| с | ||
| е | ||
| h | ||
| а | ||
| k | ||
| m | ||
| b |
Таблица 8.3. Пример кодировки одних И тех же символов различными кодами
| Символ | Частота появления | Код |
| с | ||
| е | ||
| h | ||
| • ¦ | ||
| а | ||
| k | ||
| m | ||
| Ь |
Суть метода Хаффмена сводится к следующему. Символы, встречающиеся в файле, выписываются в столбец в порядке убывания вероятностей (частоты) их появления. Два последних символа объединяются в один с суммарной вероятностью. Из полученной новой вероятности и вероятностей новых символов, не использованных в объединении, формируется новый столбец в порядке убывания вероятностей, а две последние вновь объединяются. Это продолжается до тех пор, пока не останется одна вероятность, равная сумме вероятностей всех символов, встречающихся в файле.
Таблица 8.4. Кодирование методом Хаффмена
| Символ | Частота появления | Вспомогательные столбцы |
| с | 22 22 26 32 42 58 100 | |
| в | 20 20 22 26 32 42 | |
| h | 16 16 20 22 26 | |
| I | 16 16 16 20 | |
| а | 10 16 16 | |
| k | 10 16 | |
| m | ||
| b |
Таблица 8.5. Коды символов для кодового дерева на рис. 8.1
| Символ | Код |
| с | |
| е | |
| h | |
| а | |
| k | |
| m | |
| b |
Процесс кодирования с использованием метода Хаффмена поясняется табл. 8.4. Для составления кода, соответствующего данному символу, необходимо проследить путь перехода знака по строкам и столбцам таблицы кода.
Более наглядно принцип действия метода Хаффмена можно представить В виде кодового дерева (рис. 8.1) на основе табл. 8.4. Из точки, соответствующей сумме всех вероятностей (в данном случае она равна 100), направляются две ветви. Ветви с большей вероятностью присваивается единица, с меньшей — нуль. Продолжая последовательно разветвлять дерево, доходим до вероятности каждого символа.
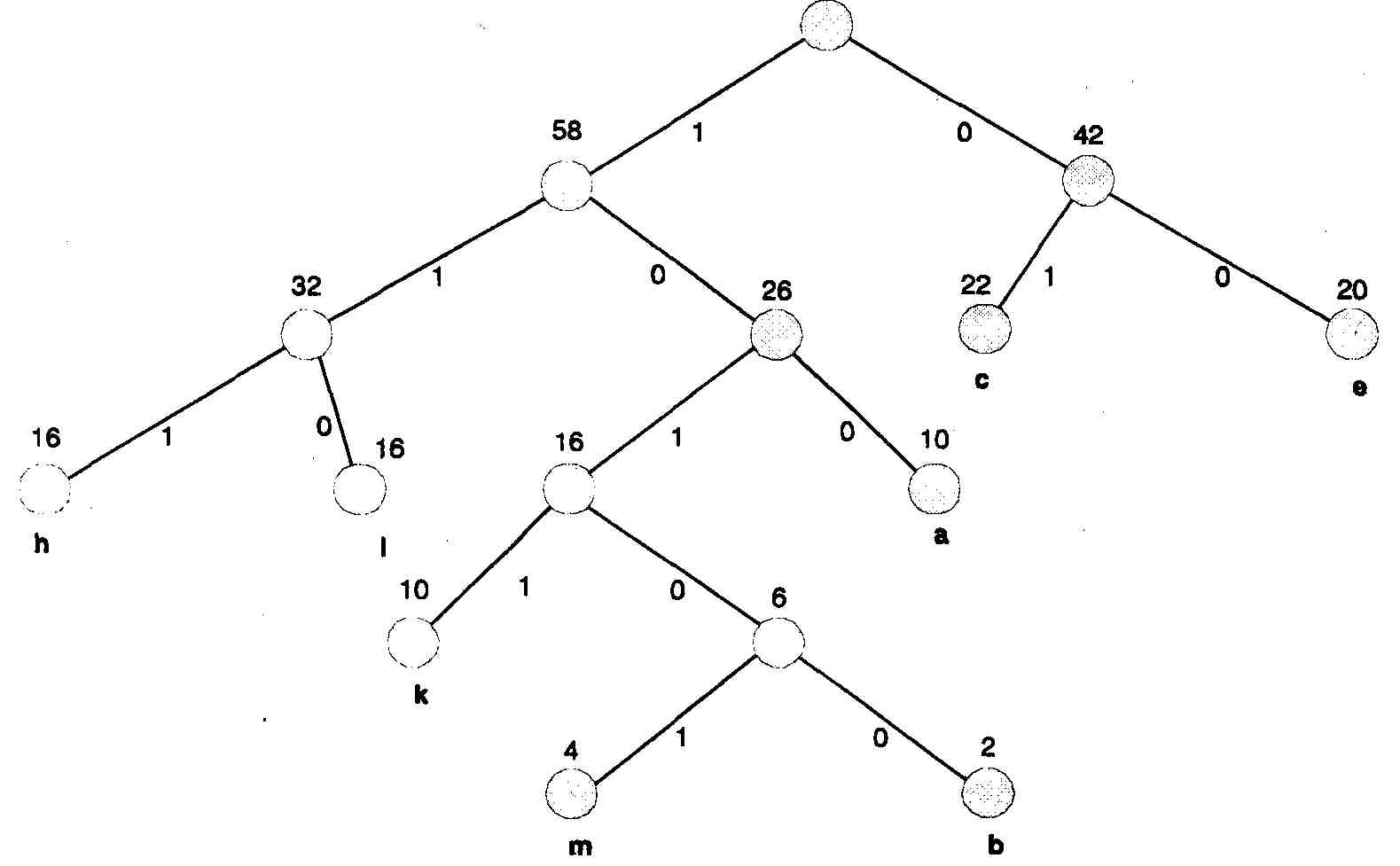
Рис. 8.1. Кодовое дерево для кода Хаффмена
Теперь, двигаясь по кодовому дереву сверху вниз, можем записать для каждого символа соответствующий код (табл. 8.5).
Алгоритм LZW
Непосредственным предшественником алгоритма LZW явился алгоритм LZ78, опубликованный в 1978 г. Этот алгоритм воспринимался как математическая абстракция до 1984 г., когда Терри Уэлч (Terry A. Welch) опубликовал свою работу с модифицированным алгоритмом, получившим в дальнейшем название LZW (Lempel-Ziv-Welch).
Алгоритм LZW построен вокруг так называемой таблицы фраз (словаря), которая отображает строки символов сжимаемого сообщения в коды фиксированной длины, равные 12 бит. Таблица обладает свойством предшествования, то есть для каждой фразы словаря, состоящей из некоторой фразы w и символа К, фраза w тоже содержится в словаре.
Алгоритм работы кодера LZW следующий:
Проинициализировать словарь односимвольными фразами, соответствующими символам входного алфавита;
Прочитать первый символ сообщения в текущую фразу *г;
Шаг алгоритма:
Прочитать очередной символ сообщения К:
Дата добавления: 2016-05-30; просмотров: 3139;











