Кинетическая, потенциальная и полная энергии гармонических колебаний

Основные характеристики колебательного движения

Процессы точно или приблизительно повторяющиеся через одинаковые промежутки времени называются колебаниями.В зависимости от физической природы различают механические, электромагнитные и другие виды колебаний. Несмотря на разную природу колебаний, в них обнаруживаются одни и те же физические закономерности, они описываются одними и теми же математическими уравнениями и исследуются общими методами, разработка и применение которых составляют задачу теории колебаний.

В данном курсе физики мы будем изучать два наиболее распространенных класса колебаний: механические и электрические.

Среди разнообразных колебаний основную и существенную роль играют так называемые гармонические колебания, то есть такие, при которых колеблющаяся величина изменяется с течением времени по закону синуса или косинуса.

Рассмотрим гармонические колебания на примере колеблющейся точки.

Пусть точка вращается по окружности радиуса А с угловой скоростью ω₀ (рис.5.1).

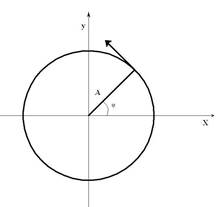
Рис.5.1.

Если точку спроецировать на оси X и Y, то ее проекции будут совершать колебания и удовлетворяют следующим уравнениям соответственно

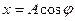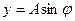, (5.1)

где, φ= ω₀t + φ₀ – фаза колебаний

Тогда

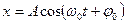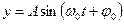и (5.2)

где х и y – смещения колеблющейся точки от положения равновесия;

А – амплитуда колебания (максимальное смещение);

φ₀ – начальная фаза (при t = 0);

ω₀ – круговая (циклическая) частота колебаний.

Точка совершает одно полное колебание за время Τ, называемое периодом колебания. Частота колебаний ν (число колебаний в единицу времени) есть 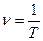. Между указанными величинами существует взаимосвязь

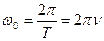(5.3)

Геометрический смысл параметров уравнений (5.2) можно объяснить с помощью векторных диаграмм. Выберем на оси Х точку О и из этой точки под углом φ₀ проведем вектор А. Будем вращать вектор А с угловой скоростью ω₀ и тогда его проекция на ось будет смещаться на величину x (рис. 5.2).

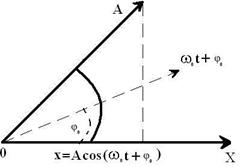
Рис.5.2.

Колеблющаяся точка обладает скоростью и ускорением. Скорость материальной точки

(5.4)

Ускорение материальной точки

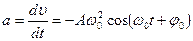(5.5)

С учетом формулы (5.2) получим

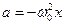(5.6)

Сравнивая уравнения (5.2), (5.4) и (5.5) замечаем, что скорость опережает смещение на π/2. Фазы ускорения и смещения различаются на π (изменяются в противофазе). Графические зависимости смещения, скорости и ускорения от времени показаны на рис.5.3.

Умножив обе части равенства уравнения (5.6) на массу m материальной точки получим

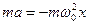(5.7)

Используя II закон Ньютона, получаем

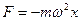(5.8)

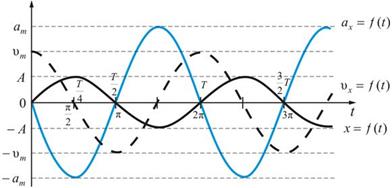
Рис.5.3.

Таким образом, чтобы совершались гармонические колебания на материальную точку должна действовать сила F, пропорциональная смещению x, которая возвращает ее в положение равновесия

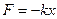(5.9)

где, k – некоторый коэффициент (зависящий от свойств колеблющейся системы) и называемой жесткостью.

Из уравнения (5.7) и (5.8) видно, что .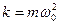

Кинетическая, потенциальная и полная энергии гармонических колебаний

Полная энергия Е колеблющейся материальной точки равна сумме кинетической Е_к и потенциальной Е_п энергий

Е = Е_к + Е_п (5.10)

Кинетическую энергию можно найти, зная массу m и скорость u

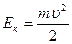(5.11)

учитывая, что

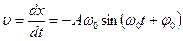
получаем

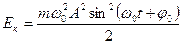(5.12)

Выражение для потенциальной энергии можно найти из соотношений между потенциальной энергией и силой.

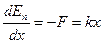
или

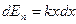(5.13)

Отсюда

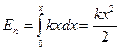(5.14)

Учитывая, что 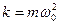и 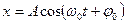получаем

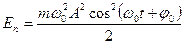(5.15)

Полную энергию получим сложив (5.12) и (5.15)

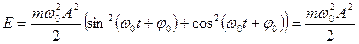(5.16)

Таким образом, полная энергия пропорциональна квадрату амплитуды колебаний.

Из формул (5.12) и (5.15) видно, что когда 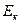увеличивается Е_п уменьшается и наоборот.

5.3. Уравнение гармонических колебаний.
Маятники

На колеблющуюся материальную точку массой m действует возвращающая сила F = - kx. Эта сила вызывает ускорение 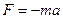. Равенство этих сил позволяет записать

ma = -kx (5.17)

где, k – жесткость системы, 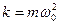; х – смещение; а – ускорение материальной точки.

Сделав соответствующие подстановки в (5.17), получим

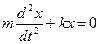или 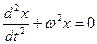(5.18)

Уравнение (5.18) представляет собой дифференциальное уравнение второго порядка незатухающих гармонических колебаний материальной точки.

Решением этого дифференциального уравнения как раз и является уравнение (5.2): .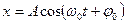

Колебания любого гармонического осциллятора (или гармонического вибратора) описываются дифференциальным уравнением второго порядка

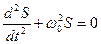(5.19)

Решением этого уравнения является

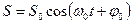(5.20)

где S₀ – амплитудное (максимальное) значение параметра S.

Примерами гармонических осцилляторов являются маятники, колебательный контур.

В качестве примера малых колебаний рассмотрим колебания маятников.

Пружинный маятник

Груз массой m, подвешенный на упругой пружине представляет собой пружинный маятник (рис.5.4). Если груз оттянуть вниз и отпустить, то под действием силы F = -kx маятник будет совершать колебания; k – коэффициент жесткости (в данном случае коэффициент упругости).

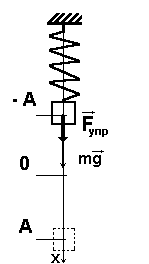
Рис.5.4.

Уравнение движения маятника имеет вид

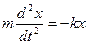или ,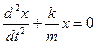

Его решением является

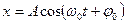
Это значит, что пружинный маятник совершает гармонические колебания с циклической частотой ω₀

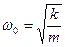, с другой стороны .

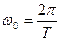Период колебаний пружинного маятника

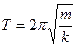(5.21).

Физический маятник

Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг оси, не проходящей через центр масс. При отклонении маятника относительно оси О угол α, на него действует М – момент возвращающей силы 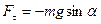(рис.5.5)

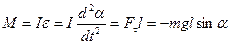(5.22)

где, I – момент инерции относительно оси О;

l – плечо силы F_τ; при малых углах .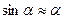

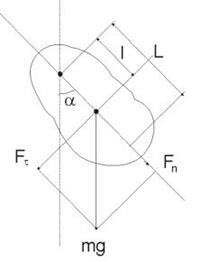
Рис.5.5.

Из (5.22) получаем дифференциальное уравнение

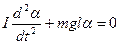
Или

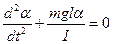(5.23)

Сравнив уравнение (5.23) с уравнением гармонического осциллятора (5.19), получим

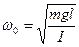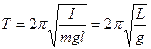, (5.24)

где, 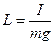– приведенная длина физического маятника.

От точки подвеса О на линии ОС на расстоянии L находится точка О₁, называемая центром качения. Точки О и О₁ обладает свойством взаимозаменяемости.