Выбор клетки, в которую необходимо послать перевозку
Транспортная задача является частным случаем задачи линейного программирования, поэтому алгоритм ее решения также следует общим принципам алгоритма симплексного метода решения задач на минимум.
Если отождествлять занятые клетки с переменными, входящими в базис, а незанятые - с независимыми, варьируемыми переменными, то в транспортной задаче загрузке (ввод в базис) подлежит та клетка, которой соответствует max[(Ui+Vj)-Сij].
В рассматриваемом примере mах(1;6;1) = 6, клетку А2В4 необходимо сделать занятой. Для этого сначала надо определить, сколько единиц груза может быть в нее перераспределено (аналог – определить максимально допустимое увеличение выбранной независимой переменной).
Построение цикла и определение величины перераспределения груза. Основной принцип перераспределения – неизменность построчных и постолбцовых сумм. Основная задача – построить цикл и найти максимальною величину груза 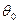 , которую можно было бы перераспределить между клетками цикла без появления отрицательных перевозок. Для этого отмечаем знаком «+» незанятую клетку (А2В4), которую требуется загрузить. Это означает, что клетка присоединяется к занятым клеткам. В таблице занятых клеток стало m+n, поэтому появляется цикл, все вершины которого, за исключением клетки, отмеченной знаком «+», находятся в занятых клетках, причем этот цикл единственный.
, которую можно было бы перераспределить между клетками цикла без появления отрицательных перевозок. Для этого отмечаем знаком «+» незанятую клетку (А2В4), которую требуется загрузить. Это означает, что клетка присоединяется к занятым клеткам. В таблице занятых клеток стало m+n, поэтому появляется цикл, все вершины которого, за исключением клетки, отмеченной знаком «+», находятся в занятых клетках, причем этот цикл единственный.
Отыскиваем цикл (алгоритмически самостоятельная задача) и, начиная движение от клетки, отмеченной знаком «+», поочередно проставляем знаки «-» и «+» (принцип неизменности сумм). Затем находим 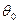 = min(xij), где xij - перевозки, стоящие в вершинах цикла, отмеченных знаком «-».
= min(xij), где xij - перевозки, стоящие в вершинах цикла, отмеченных знаком «-».
В рассматриваемом примере знаком «-» помечены клетки (А3В4), (А4В5), (А2В2). Отсюда 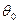 = min(0, 50, 50)=0. Напомним, что
= min(0, 50, 50)=0. Напомним, что 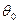 определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение
определяет, сколько единиц груза можно перераспределить по найденному циклу. Значение 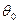 записываем в незанятую клетку (А2В4), отмеченную знаком «+», двигаясь по циклу, вычитаем
записываем в незанятую клетку (А2В4), отмеченную знаком «+», двигаясь по циклу, вычитаем 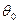 из объемов перевозок, расположенных в клетках, которые отмечены знаком «-», и прибавляем к объемам перевозок, находящихся в клетках, отмеченных знаком «+». Если
из объемов перевозок, расположенных в клетках, которые отмечены знаком «-», и прибавляем к объемам перевозок, находящихся в клетках, отмеченных знаком «+». Если 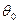 соответствуют несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было m=n- 1.
соответствуют несколько минимальных перевозок, то при вычитании оставляем в соответствующих клетках нулевые перевозки в таком количестве, чтобы во вновь полученном опорном плане занятых клеток было m=n- 1.
В рассматриваемом примере нулевую перевозку необходимо переместить в клетку А2B4, остальные числа при вычитании и прибавлении нуля, очевидно, не изменятся. В ячейке А3B4 ноль, как значимая цифра, отменяется.
В результате перераспределения 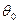 получен новый опорный невырожденный план, который снова подлежит проверке на оптимальность. Для проверки на оптимальность нового опорного плана необходимо вновь построить систему потенциалов и проверить выполнение условия оптимальности для каждой незанятой клетки, т.е. процедура оптимизации повторяется, (табл. 8.7). Расчеты выполняются до тех пор, пока повсюду не будет соблюдаться условие(8.29).
получен новый опорный невырожденный план, который снова подлежит проверке на оптимальность. Для проверки на оптимальность нового опорного плана необходимо вновь построить систему потенциалов и проверить выполнение условия оптимальности для каждой незанятой клетки, т.е. процедура оптимизации повторяется, (табл. 8.7). Расчеты выполняются до тех пор, пока повсюду не будет соблюдаться условие(8.29).
Таблица 8.7
| Поставщики | U | Потребители | Запасы | |||||||||
| B1 | B2 | B3 | B4 | B5 | ||||||||
| V1= | V2= | V3= | V4= | V5= | ||||||||
| А1 | -6 | 10 | 7 | 4 | - | 1 | + | 4 | a2 | |||
| U1 | - |  - -
| 100 | 100 | ||||||||
| А2 | -1 | 2 | - | 7 | 10 | + | 6 | 11 | a2 | |||
| U2 | 200 | 50 | 250 | |||||||||
| А3 | -11 | 8 | 5 | 3 | 2 | 2 | a1 | |||||
| U3 | - | - | - | 200 | 200 | |||||||
| А4 | 11 | + | 8 | 12 | 16 | - | 13 | a2 | ||||
| U4 | - | 150 | 100 | - | 50 | 300 | ||||||
| Спрос | 200 | 200 | 100 | 100 | 250 | 850 |
Интересно заметить, что на втором этапе (табл. 8.7) загрузка ячейки А1В5 составляет 50 ед. Эти 50 ед. выводят из базы сразу две ячейки А4В5, и А2В2, то в одной из них, например А2В2 устанавливается активный ноль.
Окончательная таблица имеет вид табл. 8.8. Полученный план является оптимальным. Его стоимость равна 4150 ед.
Таблица 8.8
| Поставщики | U | Потребители | Запасы | |||||||||
| B1 | B2 | B3 | B4 | B5 | ||||||||
| V | V1= | V2= | -6 | V3= | -10 | V4= | V5= | |||||
| А1 | -6 | 10 | 7 | 4 | 1 | 4 | 100 | |||||
| U1 | 50 | |||||||||||
| А2 | -1 | 2 | 7 | 10 | 6 | 11 | 250 | |||||
| U2 | 200 | |||||||||||
| А3 | -8 | 8 | 5 | 3 | 2 | 2 | 200 | |||||
| U3 | 200 | |||||||||||
| А4 | 11 | 8 | 12 | 16 | 13 | 300 | ||||||
| U4 | 200 | 100 | ||||||||||
| спрос | 200 | 200 | 100 | 100 | 250 | 850 |
Дата добавления: 2020-07-18; просмотров: 603;











