Построение системы потенциалов

<60 61 626364 65 66 >

Рассмотрим алгоритм метода потенциалов и одновременно проиллюстрируем его применение на опорном плане, полученном в
табл. 8.5. Для этого к таблице добавим строку и столбец, в которых записывают значения потенциалов (в результате получим макет табл. 8.6).

Таблица 8.6

Поставщики	U	Потребители	Запасы
B₁	B₂	B₃	B₄	B₅
А₁	-12		10		7		4		1		4	a₂
U₁	-		-		-		100		-
А₂	-1		2	-	7		10	+	6		11	a₂
U2	200		50		(1)		(6)		(1)
А₃	-11		8		5		3	-	2	+	2	a₁
U3	-		-		-				200
А₄			11	+	8		12		16	-	13	a₂
U4	-		150		100		-		50
спрос
V		V₁=		V₂=		V₃=		V₄=		V₅=

Систему потенциалов можно построить только для невырожденного опорного плана. Такой план содержит m+n-1 занятых клеток, поэтому для него можно составить систему из m+n-1 линейно независимых уравнений вида (8.28) с m+n неизвестными. Уравнений на одно меньше, чем неизвестных, поэтому система является неопределенной и одному неизвестному придают нулевое значение. После этого остальные потенциалы определяются однозначно. В случае вырожденности опорного плана его дополняют до невырожденного фиктивно нулевыми элементами.

Можно построить и решить относительно потенциалов систему линейных уравнений, однако специфика транспортной задачи позволяет предложить более простые и эффективные алгоритмы, при этом, как правило, используется соотношение 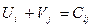. В частности, если известен потенциал U_i, тогда .

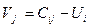Рассмотрим пример, представленный табл. 8.6. С целью наиболее эффективного использования произвольно заданного нулевого потенциала выбирается строка, которая содержит наибольшее количество занятых клеток (строка А₄). Полагаем U₄= 0. В строке А₄ три занятых клетки (А₄В₂, А₄В₃ и А₄В₅), которые связывают соответственно потенциал U₄ с потенциалами V₂, V₃, V₅. Определим эти потенциалы: V₂= С₄₂ – U₄ = 8- 0 = 8; V₃= С₄₃ – V₄ = 12- 0=12; V₅= С₄₅ – U₄ = 13- 0=13.

С помощью потенциала U₄ определить еще какой-нибудь неизвестный потенциал невозможно, поэтому как либо помечаем его, например, символом *. Теперь поочередно просматриваем столбцы В₂, B₃ и B₅, для которых потенциалы уже определены. В столбце В₂ имеется две занятые клетки (А₂В₂ и А₄В₂), которые связывают потенциал V₂ с потенциалами U₂и U₄, потенциал U₄ уже определен. Переходим к клетке А₂В₂ и с помощью С₂₂ определим неизвестный потенциал: U₂ ⁼ C₂₂ — V₂=7-8 = -1. Помечаем потенциал V₂, знаком * и переходим к столбцу B₃. В этом столбце нет занятых клеток, которые бы связывали V₃ с неизвестными потенциалами строк.

Данный процесс продолжается для остальных строк и столбцов. Однако после его прерывания (невозможно определить еще какие-либо неизвестные потенциалы) остались неопределенными потенциалы U₁ и V₄. Это произошло потому, что опорный план является вырожденным. Для устранения вырожденности количество занятых клеток дополняется до m+n-1, путем введения нулевых перевозок. Клетки, в которые введены нулевые перевозки, называются фиктивно занятыми.

Чтобы определить потенциалы U₁ и V₄, необходимо сделать фиктивно занятой одну из незанятых клеток либо строки A₁, либо столбца В₄, для которых один из потенциалов определен. Задача заключается в минимизации линейной целевой функции, поэтому целесообразно фиктивно занятой сделать клетку, в которой стоит наименьшая стоимость.

Просматривая стоимости, стоящие в незанятых клетках строки A₁ и столбца В₄, выбираем наименьшую (min(C_ij)= 2), которая соответствует клетке А₃В₄, в нее записываем нуль и считаем занятой. Теперь клетка А₃В₄связывает потенциал с потенциалом U₃, V₄= 2 - (-11) =13. Затем находим U₁ = С₁₄ — V₄ = 1-13 =- 12.

Система потенциалов построена. Проверяем правильность построения системы. Для этого просматриваем занятые клетки строк и для каждой из них определяем сумму потенциалов. Если для всех занятых клеток выполняется равенство (8.28), то система построена правильно, в противном случае ее надо построить заново или изменить так, чтобы условие (8.28) выполнялось.

Проверка выполнения условия оптимальности для незанятых клеток

Для каждой незанятой клетки проверяется условие (8.29), т. е. сравнивается сумма соответствующих клетке потенциалов со стоимостью. Если для всех незанятых клеток неравенства выполняются, то план является оптимальным. Если нет, то план является неоптимальным. Для каждой клетки, в которой не выполняется условие оптимальности, определяется разность (U_i + V_j) - C_ij > 0, которая записывается в левый нижний угол этой же клетки. В рассматриваемом примере (табл. 8.6) имеются три клетки, в которых нарушено условие оптимальности; разности соответственно равны 1, 6 и 1.