Метод минимальной стоимости.
Суть метода заключается в том, что процесс построения начального плана начинается из клетки с минимальной стоимостью. Сюда помещают меньшее из чисел ai или bj. Затем из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжается, пока все запасы не будут распределены, а потребности удовлетворены.
Читателю рекомендуется с помощью этого метода составить опорный план уже рассмотренной задачи (табл. 8.5).
Таблица 8.5
| Постав-щики | Потребители | Запасы | |||||||||
| B1 | B2 | B3 | B4 | B5 | |||||||
| А1 | 10 | 7 | 4 | 1 | 4 | a2 | |||||
| - | - | - | 100 | - | 100 | ||||||
| А2 | 2 | 7 | 10 | 6 | 11 | a2 | |||||
| 200 | 50 | - | - | - | 250 | ||||||
| А3 | 8 | 5 | 3 | 2 | 2 | a1 | |||||
| - | - | - | - | 200 | 200 | ||||||
| А4 | 11 | 8 | 12 | 16 | 13 | a2 | |||||
| - | 150 | 100 | - | 50 | 300 | ||||||
| спрос | 200 | 200 | 100 | 100 | 250 | 850 |
План не содержит циклов и состоит из семи положительных перевозок, следовательно, является вырожденным опорным планом. Определим его стоимость:
Z=100·1 +200·2+50·7+200·2+150·8+100·12+ 50·13=4300 (ед.), что значительно меньше, чем аналогичная величина, полученная первым методом, следовательно, этот план ближе к оптимальному.
Метод потенциалов
Построенный опорный план транспортной задачи как задачи линейного программирования можно было бы довести до оптимального с помощью симплексного метода. Однако из-за громоздкости симплексных таблиц, содержащих mn неизвестных, и большего объема вычислительных работ для получения оптимального плана используются более простые методы. Самым распространенным является метод потенциалов (модифицированный распределительный метод).
В основе данного метода лежит теорема, являющаяся, по существу, отражением теоремы двойственности применительно к транспортной задаче.
Теорема. Если план 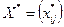 транспортной задачи является оптимальным, то ему соответствует система из m+n чисел
транспортной задачи является оптимальным, то ему соответствует система из m+n чисел 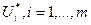 и
и 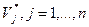 , удовлетворяющих условиям
, удовлетворяющих условиям
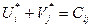 ,
, 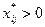 ;
;
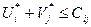 ,
, 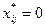
(i=1,…,m; j=1,…,n)
Числа 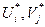 называются потенциалами соответственно поставщиков и, потребителей.
называются потенциалами соответственно поставщиков и, потребителей.
Действительно, условия
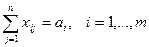 ;
;
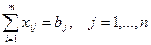
определяют m+n ограничений типа «равенство». Каждому равенству i соответствует двойственная переменная Ui. а равенству j - двойственная переменная Vj . В двойственной задаче ограничивающих условий столько, сколько переменных в основной задаче, т.е. mn. В правой части двойственного ограничения - Cij.
В результате транспонирования матрицы коэффициентов в новой матрице в каждой строке имеются лишь две единицы, соответственно позиции i и j. Отсюда ограничение 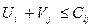 . Для большего понимания рассмотрим транспортную задачу размерностью 2х2.
. Для большего понимания рассмотрим транспортную задачу размерностью 2х2.
Дата добавления: 2020-07-18; просмотров: 656;











