Решение систем уравнений с прямоугольной матрицей коэффициентов

Выполняются n-1 исключение переменных 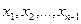. В результате остались 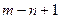уравнений с одной неизвестной x_n, т.е. .

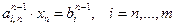В общем случае коэффициенты a и bв этих уравнениях различны. Могут отличаться и их отношения. В этом случае найти такое значение x_n, которое удовлетворяло бы всем уравнениям одновременно невозможно. Отсюда решение существует лишь в том случае, если

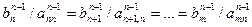(линейно зависимая СЛУ).

При этом .

СЛУ, не имеющую ни одного решения, будем называть переопределенной или противоречивой.

Число уравнений меньше числа неизвестных, m < n

Представим исходную СЛУ в виде

, ,

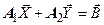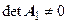(4.6)

Это всегда можно сделать методом гауссовского исключения с выбором главного элемента, например, «по блоку».

Размерность марицы определяется рангом r матрицы А. Если r<m, то оставшиеся m-r являются линейной комбинацией первых r уравнений и могут быть отброшены как незначимые.Без нарушения общности будем считать, что r=m.

Вектор 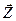неизвестных разделяется на два подвектора 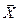и .

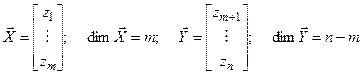
При сделанных допущениях СЛУ можно разрешить относительно :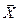

.

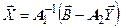Это выражение показывает, что система m линейных уравнений с n неизвестными при m < n имеет не одно, а целое множество решений. Каждое из таких решений соответствует некоторому (произвольному) значению вектора .

Компоненты вектора называются независимыми, а компоненты вектора 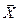– зависимыми компонентами вектора решений. Число r = n – mназывается количеством степеней свободы системы. Каждое дополнительное независимое уравнение увеличивает ранг матрицы коэффициентов и уменьшает количество степеней свободы на единицу.

Среди множества возможных решений рассматриваемой системы линейных уравнений целесообразно выделить так называемые базисные решения, соответствующие нулевым значениям независимых переменных:

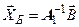
С термином “базисное” решение системы уравнений связаны названия неизвестных. Вектор зависимых переменных 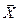называется вектором базисных переменных, а вектор независимых переменных – вектором внебазисных значений.