Итерационный метод Брауна-Робинсона

Также универсальным, но менее трудоемким по сравнению с методом линейного программирования в плане затрат вычислительных ресурсов является приближенный метод Брауна-Робинсона. Данный итерационный метод предназначен для решения любой игры G(m´n), не требуя никаких ограничений на элементы матрицы игры.

Метод базируется на многократном разыгрывании игры и подсчете верхней и нижней оценок цены игры с занесением результатов в таблицу специального вида (табл. 3.11):

Таблица 3.11

k	i	B1	…	Bn	j	A1	…	Am	V		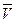V*

Каждая строка таблицы соответствует однократному розыгрышу игры (партии игры).

Поясним записи в соответствующих позициях:

· k — номер партии (итерации);

· i и j — номера стратегий, выбранных соответственно игроками A и B в данной партии;

· B_1, …, B_n — накопленный за k партий выигрыш игрока A при выборе им стратегии A_i в данной партии и ответе игроком B соответственно стратегиями B_1, …, B_n;

· A_1, …, A_m — накопленный за k партий выигрыш игрока A при выборе игроком B стратегии B_j в данной партии и ответе игроком A соответственно стратегиями A_1, …, A_m;

· V —нижняя оценка цены игры (минимальный накопленный выигрыш, поделенный на k);

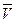· — верхняя оценка цены игры (максимальный накопленный выигрыш, поделенный на k);

· .

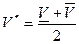В [6] доказано, что при k à ¥: V^*à V, , ,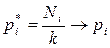

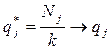где V – цена игры, N_i и N_j – число применений соответственно стратегий А_i и B_j за k партий, p_i и q_j – значения вероятностей в оптимальных стратегиях S_A =(p_i), i =1, …, m, S_B =(q_j), j =1, …, n,игроков A и B соответственно.

Проиллюстрируем метод на примере игры G(3´3), представленной табл. 3.12.

Таблица 3.12

Bj Ai	B1	B2	B3
A1
A2
A3

Требуется найти решение – пару оптимальных смешанных стратегий (S_A, S_B), S_A =(p₁, p₂, p₃), S_B =(q₁, q₂, q₃), и цену игры V.

Будем искать пару смешанных стратегий S_A =(p₁, p₂, p₃), p₁ + p₂ + p₃ = 1, S_B =(q₁, q₂, q₃), q₁ + q₂ + q₃ = 1 и цену игры V.

Построим табл. 3.13 для первых десяти итераций.

Таблица 3.13

k	i	B1	B2	B3	j	A1	A2	A3	V	`V	V*
1											4,5
2									4,5		6,75
3									3,67		4,84
4									2,75	5,5	4,13
5									4,0	6,6	5,3
6									4,84	5,5	5,17
7									4,43	5,14	4,79
8									5,0	5,61	5,30
9									4,45	5,11	4,78
10									4,90	5,30	5,1

Поясним процесс заполнения табл. 3.13.

Пусть начинает (k =1) игрок A и выбирает на первом шаге стратегию А₁. Его выигрыш в зависимости от выбора игрока B может равняться 9 (при выборе стратегии B₁), 0 (при выборе B₂) или 11 (при выборе B₃). Поскольку теперь выбор за игроком B (а он заинтересован в минимизации выигрыша игрока A), то выделим (жирным шрифтом) минимальный выигрыш 0, соответствующий стратегии B₂. Следовательно игроку B выгоднее всего ответить стратегией B₂, что, в свою очередь, может привести к выигрышу игрока A при его ответе в следующей партии, равному 2 (при выборе стратегии A₁), 9 (A₂) или 0 (A₃). Так как игрок A заинтересован в максимизации выигрыша, то выделим максимальный выигрыш 9 (для A₂). Соответствующие значения V, 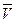и V^* равны 0; 9 и 4,5.

Во второй партии (k =2) игроку A,следовательно,выгодно выбратьстратегию A₂,которая позволит ему накопить выигрыш, равный соответственно 11 (для B₁), 9 (для B₂) или 11 (для B₃) и т.д. Заметим, что для k =4в столбцах А₁и А₃ получаются одинаковые накопленные выигрыши (22), поэтому игрок A в пятой партии может выбрать как стратегию А₁, так и А₃.

К сожалению (что видно и по табл. 3.12), сходимость данного метода довольно слабая, но существуют методы ее ускорения. Критерием останова можно выбрать достаточную стабильность величины V^* при увеличении числа итераций.

Для рассматриваемого примера в итоге получим:

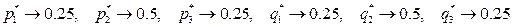и 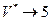, что соответствует точному решению, полученному, например, методом Лагранжа.

Как уже отмечалось, сравнительно невысокая трудоемкость данного метода часто делает его более предпочтительным по сравнению с методом линейного программирования (например, симплекс-методом) при решении задач линейного программирования (после их сведения к соответствующей теоретико-игровой задачи) большой размерности.