Процессы конечной длительности в импульсных системах.

Протекание переходных процессов в импульсных системах имеет свои особенности. В частности, здесь оказываются возможными процессы, затухающие за конечное время, так называемые процессы конечной длительности. Определим условия их возникновения в дискретной системе с передаточной функцией w(z). Рассмотрим импульсную переходную функцию 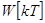установим, когда возможно выполнение равенства

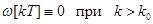(95)

Пусть передаточная функция w(z) является дробно-рациональным выражением, т.е.

.

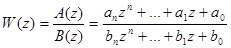Умножив числитель и знаменатель на 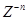, приведем передаточную функцию к виду

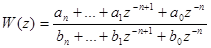
Функции 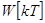и w(z) связаны между собой z-преобразованием, т.е. с учетом равенства (95)

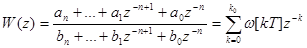(96)

Очевидно, что равенство (96) возможно при выполнении условий

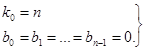(97)

Таким образом, выполнение условий (97) влечет за собой выполнение равенства (95). С учетом равенства (95) при 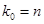из выражения (91) имеем

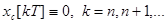
т.е. свободные процессы в системе заканчиваются за n шагов квантования, где n- порядок системы.

После этого в системе устанавливается вынужденный процесс 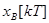. Наличие процессов с конечной длительностью, т.е. выполнение условий (97), обеспечивается надлежащим выбором параметров исходной системы или параметров дополнительного корректирующего устройства. Отметим, что характеристическое уравнение такой системы имеет вид

,

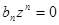т.е. устойчивость дискретной САУ гарантируется.