Установившиеся ошибки при типовых входных сигналах.

Найдем установившуюся ошибку системы 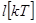. Из теории непрерывных САУ известно, что величина установившейся ошибки определяется соотношением степени полинома входного воздействия с порядком астатизма разомкнутой системы. Аналогичное положение сохраняется и для дискретных систем. Из п.2.3 следует, что полюсу p=0 передаточной функции ПНЧ соответствует полюс z=1 Z-передаточной функции W(z) , причем порядки этих полюсов (степени астатизма) совпадают (см. зависимость (24)). Тогда Z-передаточная функция W(z) дискретной системы, приведенная непрерывная часть которой обладает астатизмом порядка 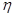, может быть записана в виде

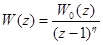
где 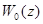- дробно-рациональная функция, причем z=1 не входит в число ее нулей или полюсов.

Определим передаточную функцию ошибки замкнутой импульсной системы:

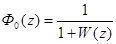
или

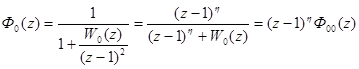
где .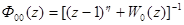

Установившееся значение сигнала ошибки найдем по теореме о предельном значении решетчатой функции:

.

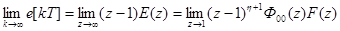где .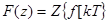

Из формулы (98) и таблиц z-преобразования получим

,

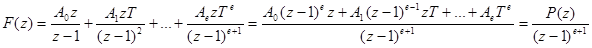где P(z) - полином степени 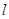, причем .

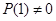Тогда зависимость для установившейся ошибки принимает вид

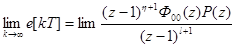(99)

Из анализа формула (99) видно, что могут представиться три случая:

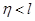- порядок астатизма меньше степени полинома входного воздействия. Тогда

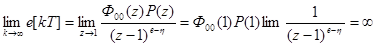
т.е. ошибка неограниченно увеличивается с увеличением времени»

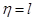- порядок астатизма равен степени полинома входного воздействия. Тогда

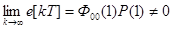
т.е. установившееся значение ошибки является постоянной величиной, отличной от нуля;

3) 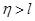- порядок астатизма больше степени полинома входного воздействия. Тогда

,

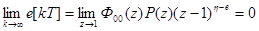т.е. в этом случае установившееся значение ошибки равно нулю.

Если система является статической 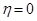, то установившаяся ошибка при отработке ступенчатого сигнала

.

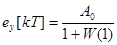Величина W(1) представляет собой коэффициент передачи разомкнутой дискретной системы K. Нетрудно показать, что для случая экстраполятора нулевого порядка он совпадает со значением коэффициента передачи приведенной непрерывной части 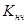. Таким образом, установившаяся ошибка статической системы на постоянный сигнал определяется по выражению

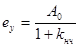
Для системы с астатизмом первого порядка 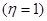установившаяся ошибка на линейно нарастающий сигнал 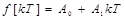определяется по выражению

,

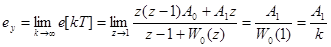где К - коэффициент передачи системы по скорости,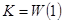

В импульсных системах в установившемся режиме могут возникать колебания внутри интервала квантования (так называемые "скрытые колебания"). Отметим, что в линейных импульсных системах с экстраполятором нулевого порядка в качестве формирующего звена появление таких колебаний принципиально невозможно. Возникновение "скрытых колебаний" связано с использованием формирующего звена, поддерживающего величину импульса на интервале 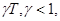т.е. звена с передаточной функцией

,

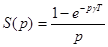При необходимости их исследования выходной сигнал рассматривают в смещенные моменты времени 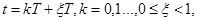, т.е. используют смешенные Z-передаточные функци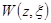и и

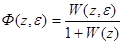
дискретной системы.