Расчет давления в атмосфере: барометрические формулы

Барометрические формулы. Приведенный выше градиент давления используется для расчета изменения давления лишь при очень малых приращениях высоты. Для многих же задач расчеты приходится проводить для слоев, измеряемых сотнями и тысячами метров. Для этой цели существуют так называемые барометрические формулы, выведенные из основного уравнения статики для различных условий изменения с высотой температуры и плотности воздуха. Рассмотрим сначала три простейшие модели атмосферы: однородную, изотермическую и политропную.

Однородная атмосфера. Однородной атмосферой называется такая, в которой плотность воздуха с высотой не изменяется, т. е. р (z) = const. Проинтегрируем уравнение статики в пределах от уровня моря (z = 0) до высоты H, на которой давление р = 0;

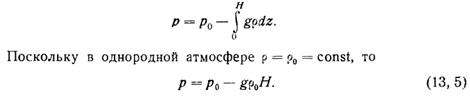
Следовательно, в однородной атмосфере давление с высотой падает по линейному закону. В реальных условиях подобное допущение может быть сделано только для гидросферы, однако понятие однородной атмосферы используется в различных расчетных формулах.

Определим высоту однородной атмосферы, положив в формуле (13, 5) р = 0, тогда

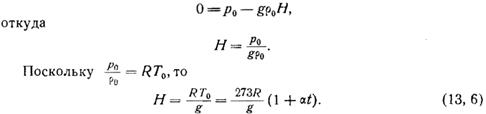
Отсюда видим, что высота Я однородной атмосферы зависит только от температуры воздуха на поверхности Земли и при t = 0° будет

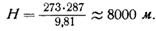
Поскольку плотность однородной атмосферы постоянна, а давление с высотой быстро падает, то и температура должна быстро падать, что видно из уравнения

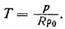
Но так как давление в однородной атмосфере изменяется с высотой линейно, то и температура также падает линейно, т. е.

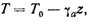
где 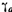— вертикальный градиент температуры в однородной атмосфере, называемый градиентом авто конвекции, он равен 3°,42/100 м.

Изотермическая атмосфера. Изотермической атмосферой называется такая, в которой температура на всех высотах постоянная. Интегрирование основного уравнения статики для условия постоянства температуры по высоте, т. е. когда

T_z - Т₀ = const,

дает следующую формулу для изменения давления с высотой

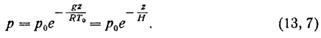
Эта модель атмосферы также иногда применяется в расчетных формулах. Из формулы (13, 7) видно, что изотермическая атмосфера бесконечна, так как р = 0 при z = ∞.

Политропная атмосфера. Политропной атмосферой называется такая атмосфера, в которой температура с высотой убывает по линейному закону. Если Т = T₀ — ϒ_z и ϒ = const, то для изменения давления с высотой получаем формулу политропной атмосферы:

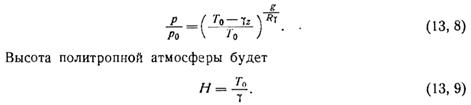
При Т₀ = 273° и ϒ = 1 °/100 м Н = 27,3 км; при ϒ = 0°,5/100 м и той же Т₀ И = 54,6 км. При ϒ = 3°,42/100 м H = 8 км, т. е. высота политропной атмосферы равна высоте однородной атмосферы.

Барометрическая формула Лапласа имеет следующий вид:

Полная барометрическая формула (13, 10) применяется только для высокоточного барометрического нивелирования. Для других целей ее обычно упрощают, сообразуясь с точностью исходных данных.

Для сухого воздуха (q_m = 0) без учета зависимости ускорения силы тяжести от широты и высоты формулу (13, 10) можно привести к виду

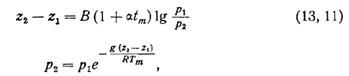
а полагая z₁ совпадающим с поверхностью Земли, получим

Барометрическая формула Бабине. Для расчета распределения давления в небольших по толщине нижних слоях атмосферы (до 2000 м) пользуются упрощенной барометрической формулой Бабине. При ее выводе основное уравнение статики атмосферы принимается в конечных разностях, а реальное распределение плотности заменяется средним ее значением. Взяв те же предпосылки, что и при выводе уравнения статики, будет иметь:

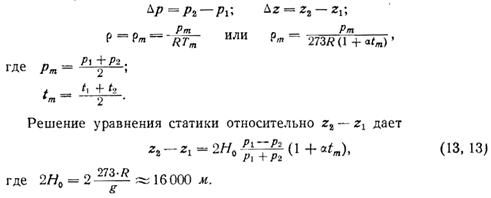
Относительные ошибки расчетов высоты с использованием упрощенной формулы не превышают 1% при условии, что толщина слоя не превосходит 2000 м. Формула (13, 13) применяется для приведения давления к уровню моря. С этой целью обычно составляются специальные таблицы, которыми на практике и пользуются.

Барометрическая ступень. Высота, на которую нужно подняться, чтобы давление упало на 1 мб, называется барометрической ступенью, т. е.

Барометрическая ступень применяется для приближенной оценки изменения давления с высотой. Из формулы (13, 14) следует, что с увеличением высоты барометрическая ступень растет, поскольку р уменьшается.

Сведения об авторах и источниках:

Автор: Н. И. Егоров, И. М. Безуглый, В. А. Мнежинский, и др.

Источник: Морская гидрометеорология

Данные публикации будут полезны для курсантав морских учебных заведений и капитанаов/штурманов гражданского флота, интересующимся глубоким пониманием гидрометеорологии