Линейные стационарные системы
В теории цифровой обработки сигналов (ЦОС) система определяется как однозначное преобразование или оператор, отображающий входную последовательность 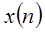 в выходную
в выходную 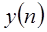 , что математически записывается в виде
, что математически записывается в виде
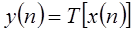 . .
| (1.14) |
Классы дискретных систем определяются путем наложения ограничений на преобразование T. Класс линейных систем определяется принципом суперпозиции. Если 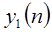 и
и 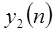 - отклики на
- отклики на 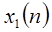 и
и 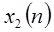 соответственно, то система линейна тогда и только тогда, когда
соответственно, то система линейна тогда и только тогда, когда
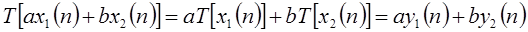
| (1.15) |
Пусть 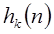 - отклик системы на
- отклик системы на 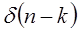 единичный импульс в момент
единичный импульс в момент 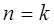 . Тогда для линейной системы можно записать
. Тогда для линейной системы можно записать
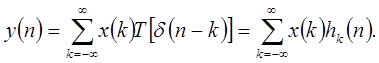
| (1.16) |
Класс стационарных систем характеризуется следующим свойством: если 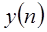 - отклик на
- отклик на 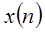 , то
, то 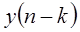 будет откликом на
будет откликом на 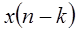 , где
, где 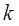 - положительное или отрицательное целое число. Для стационарной системы можем записать
- положительное или отрицательное целое число. Для стационарной системы можем записать
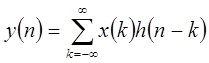 . .
| (1.17) |
Значит, любая линейная стационарная система полностью характеризуется импульсной характеристикой 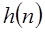 . Выражение (1.17) обычно называют сверткой. Заменой переменной в (1.17) получим другое выражение
. Выражение (1.17) обычно называют сверткой. Заменой переменной в (1.17) получим другое выражение
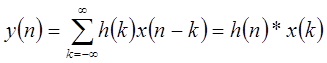
| (1.18) |
Поэтому порядок, в котором две последовательности входят в свертку, не важен. Другими словами, линейная стационарная система с входом 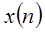 и импульсной характеристикой
и импульсной характеристикой 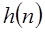 будет иметь тот же выход, что и линейная стационарная система с входом
будет иметь тот же выход, что и линейная стационарная система с входом 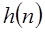 и импульсной характеристикой
и импульсной характеристикой 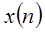 .
.
Дата добавления: 2020-06-09; просмотров: 783;











