Условные и условно-категорические силлогизмы

И в науке, и в обиходе приходится часто отмечать зависимость тех или иных явлений, событий, процессов от всякого рода обстоятельств: факторов, способных изменить течение дел, причинных воздействий, порождающих известные события, внешних влияний, которые удерживают ход вещей в известных рамках. Короче, речь идет об условиях, определяющих все, что происходит вокруг нас. Обычно условия задаются с помощью оборота "Если..., то...": "Если работа окончена, то мы можем идти", "Если орудие железное, то оно не относится к каменному веку". Суждения, в которых задаются такого рода связи, называют условными, а в символической логике импликативными, или импликациями.

Условные суждения и вместе с ними условные умозаключения стали изучаться еще в Древней Греции философами стоической школы. Правила оперирования такими умозаключениями довольно просты и легко устанавливаются.

Условные силлогизмы подразделяются на собственно условные и условно-категорические. Кроме того, они могут комбинироваться с другими умозаключениями, например с разделительными, о которых речь впереди.

Собственно условные умозаключения содержат и в посылках, и в заключении одни только условные суждения:

Если выпускается много денежных знаков, то растут денежные доходы.

Если растут денежные доходы населения, то растет покупательная способность.

Если растет покупательная способность, то растут цены.

Если растут цены, то растет инфляция.

Следовательно, если выпускается много денежных знаков, то растет инфляция.

Выражение "Если..., то..." удобно заменять стрелкой, а сами высказывания - буквами a, b, c,... Тогда получается простая символическая запись, которая означает: если a, то b, если b, то c...

a ® b.

b ® c.

a ® c.

Каждое условное суждение можно при желании заменять на общеутвердительное или общеотрицательное категорические суждения. И наоборот, общие утвердительные и отрицательные суждения можно переформулировать в условные. Отсюда появляется возможность даже категорические силлогизмы с общими посылками и заключениями представить в виде условного умозаключения:

Учебник - книга. Если вещь - учебник, то она книга.

Задачник - учебник. Если вещь - задачник, то она учебник.

Задачник - книга. Если вещь - задачник, то она книга.

Этой взаимозаменимостью пользуются в символической логике для записи категорических суждений и силлогизмов в виде формул.

Полезно обратить внимание на один парадокс условных умозаключений. Мы его продемонстрируем примером:

Если случается засуха, то следствием ее бывает неурожай.

Если бывает неурожай, то наступает угроза голода.

Если наступает угроза голода, то растет цена на продовольствие.

Если растет цена на продовольствие, то увеличивается его подвоз.

Если увеличивается подвоз продовольствия, то наступает изобилие.

Следовательно, если случается засуха, то наступает изобилие.

Несуразица в выводе получается потому, что условные умозаключения учитывают только самые общие черты соответствующих процессов взаимодействия, все остальное опускается. Интуитивно ясно, что реакция экономических механизмов на недобор урожая лишь частично компенсирует его последствия и никакого изобилия от недорода на деле не будет. Но эти количественные характеристики не задаются и не могут задаваться условными умозаключениями. Отсюда парадоксальные выводы при правильно построенном условном силлогизме.

Условно-категорическое умозаключение имеет одну из посылок и заключение, выражаемые категорическими суждениями. У него два правильных модуса, которые имеют латинские названия - modus ponens (утверждающий) и modus tollens (отрицающий). Первый из них выглядит следующим образом:

Если алмаз огранен, то он - бриллиант. a ® b

Данный алмаз огранен. a

Данный алмаз - бриллиант. b

Modus ponens

В нем от наличия основания условной связи делают вывод о наличии следствия. Название "утверждающий" происходит от того, что этим модусом условно-категорического силлогизма утверждается то, о чем говорит следствие в его посылке. Но это вовсе не означает, будто его заключение может быть только утвердительным суждением. В том случае, когда следствие в условной посылке является отрицательным, то тогда и вывод тоже звучит как отрицание. Например, возьмем утверждение, сделанное в виде такой условной посылки: "Если температура ниже нуля, то лед не тает". Добавим сюда еще одну посылку: "Температура ниже нуля". Тогда нам придется делать такой вывод по схеме утверждающего модуса, который, однако, выражается отрицательным суждением: "Лед не тает".

При отрицающем модусе вывод делается от отсутствия следствия к отсутствию порождающего его основания:

Если данный материал - стекло, то он хрупкий. a ® b

Данный материал не хрупкий.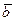

Данный материал - не стекло.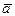

Modus tollens

Надчеркивание над буквами в символической записи умозаключения выражает отрицание, означает то же, что не-a или, точнее, неверно, что a.

И этот модус, подобно предыдущему, в принципе может давать как утвердительный по логической форме вывод, так и отрицательный. Все зависит от того, каким суждением выражается основание условной посылки. Скажем, рассуждение "Если такси не свободен, то не горит "зеленый глазок"; но "зеленый глазок" горит" приводит к утвердительному выводу: "Такси свободен". Хотя получен он по отрицающему модусу.

Суммировать приведенные соображения можно одним простым и коротким правилом:

Вывод в условно-категорическом умозаключении можно делать либо от наличия основания к наличию следствия, либо от отсутствия следствия к отсутствию основания.

Интуитивно здесь напрашиваются еще два возможных модуса, которые, однако, в действительности являются неправильными.

Если у пациента температура, то он болен. a ® b

У данного пациента нет температуры.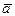

Данный пациент не болен? ?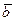

Если у пациента температура, то он болен. a ® b

Данный пациент болен. b

У данного пациента температура? a?

Неправильные модусы

На самом деле в силу многозначности причинно-следственных связей, в силу того, что одно и то же следствие может вызываться многими причинами, выводы по таким модусам в лучшем случае вероятностны, но часто бывают и ложными. Наличие температуры не доказывает, что у больного обязательно ангина, ибо и другие болезни тоже вызывают ее, и отсутствие ангины не гарантирует отсутствие повышенной температуры по тем же причинам. Только в том случае, когда связь между основанием и следствием взаимно-однозначная, то есть когда одно не бывает без другого, только тогда выводы по неправильным модусам дают верный результат. Например, условная посылка "Если год високосный, то в феврале 29 дней" позволяет строить умозаключения по всем четырем модусам, включая два неправильных.

Условно-категорическое умозаключение представляет собой один из самых элементарных шагов в выводах и доказательствах. Оно имеет чрезвычайно широкое распространение. Несмотря на его кажущуюся простоту, разобраться порой с ним бывает не так уж и легко, особенно когда посылки содержат отрицания и вдобавок выражаются длинными предложениями. Знание условных и условно-категорических силлогизмов настоятельно необходимо всякому, кто хочет овладеть законами правильного мышления.