Создание узоров построением зеркальных отображений фигуры.
Большинство людей впервые знакомятся с некоторыми принципами построения узоров, изучая детский зеркальный калейдоскоп. В калейдоскопе система из трех зеркал создает эффект нескольких шестикратных отражений набора цветных кристаллов. Математически такой принцип построения узора можно описать следующим образом. Имеется "N" выходящих из одной точки лучей - осей симметрии. Угол между лучами равен 2*PI/N. Строится первая (исходная) фигура в секторе между первым и вторым лучами. Затем строится вторая фигура как зеркальное отображение первой фигуры относительно второго луча, третья фигура, как зеркальное отображение второй фигуры относительно третьего луча и так далее. Если N - четно, то исходная фигура будет также зеркальным отражением N-й фигуры и получившийся узор будет симметричным (правильный калейдоскоп). Если нет необходимости моделировать реальные отражения, то исходную фигуру можно строить с пересечением осей симметрии и по любому количеству секторов.
 Y Y
 ось ось
  * симметрии * симметрии

   *
X *
X
|
Ниже приведен пример программы создания узора построением отражений "m" точек относительно "n" осей отражения (зеркал). Исходная фигура - замкнутая ломаная, состоящая из разноцветных отрезков прямых. Для каждой узловой точки линии определяется расстояние до центра узора (радиус r). Угол (ugol), под которым расположена узловая точка относительно горизонтальной линии, вычисляется как арктангенс отношения ординаты "x" к абсциссе "y" (в системе координат центра узора). Угол, под которым расположена отраженная точка, увеличивается на величину, равную удвоенной разности между углом наклона оси отражения и углом расположения отражаемой точки.
{ ---------- ------------ "Калейдоскоп": ------------------------
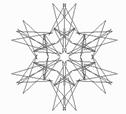
|
Строится фигура в виде ломаной линии, состоящей из "m-1" отрезков прямых и "n" зеркальных отражений этой ломаной относительно осей симметрии, проходящих через центр узора.
------------------------------------- ------------ }
Uses Graph, Crt;
type mas = array[1..40, 1..20] of integer;
Дата добавления: 2016-06-29; просмотров: 1966;











