ТЕПЛОВОЕ СОСТОЯНИЕ ЭЛЕМЕНТОВ РДТТ

Обычно задачи теплопроводности стараются упростить понижением их размерности при разумной потере точности. Элементы тепловой защиты корпусов и сверхзвуковых частей сопел представляют собой осесимметричные тонкостенные многослойные составные оболочки; толщины их малы по сравнению с длиной. Для упрощения численный процедур температурные поля таких элементов моделируют с помощью одномерного уравнения теплопроводности

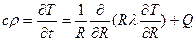. (5.17)

Начальным условием служит равномерное распределение температуры по толщине многослойной стенки 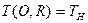. Граничным условием является баланс энергии на перемещаемой стенке

;

.

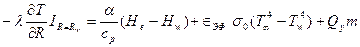
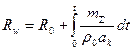На стыках слоев выполняют условия сопряжения

; .

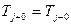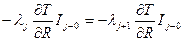Граничным условием на внешней поверхности последнего слоя (слоя защищаемой конструкции) принимают либо условие изоляции

,

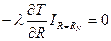либо условие теплообмена с окружающей средой без разрушения поверхностного слоя

.

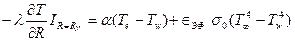Это условие отвечает условию испытания двигателя на стенде, а в полете ракеты необходимо учитывать аэродинамический нагрев конвекции,

Переизлучение стенки в окружающее пространство и возможное разру­шение внешней защиты корпуса двигателя или элемента соплового бло­ка Области применения краевых задач теплопроводности при модели­ровании процессов в РДТТ представлены в табл. 5.4.

Для тонких концевых насадок сопел большой степени расширения, выполненных из тугоплавких металлов (Mo, Nb), характерен прогрев практически без перепада температур по толщине. Пренебрегая энергией, пошедшей на нагрев насадка до искомой температуры T_w, установив­шееся значение этой температуры можно вычислить из баланса энергии (поступающие конвективные и радиационные потоки равны отводимому излучением в окружающее пространство):

.

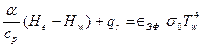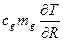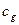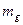Учет поглощения тепла при фильтрации газов пиролиза выполняют при допущении о температурном равновесии газовой фазы и твердого кокса с помощью конвективного члена [24], где и - теплоемкость и массовая скорость продуктов пиролиза. Такой подход исключает решение очень сложной задачи тепломассообмена в пористом теле в полной постановке, включающей уравнение движения и энергии газовой фазы совместно с уравнением теплопроводности в твердом кар­касе прококсованного слоя.

Тепловой эффект разложения связующего в концепции фронта пи­ролиза [24] (пиролиз происходит в очень узкой области при достиже­нии значения некоторой характерной изотермы Т*) связан со скоростью потери массы выражением

,

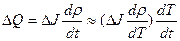где 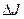— тепловой эффект фазового превращения.

Массовую скорость продукта пиролиза можно оценить по соот­ношению

,

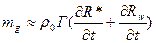где Г — доля связующего, перешедшего в газообразное состояние; R*— положение характерной изотермы.

Тогда уравнение (5.17) примет вид

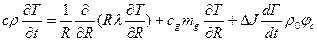, (5.18)

где 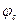- доля связующего в материале; 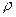₀ — начальная плотность до пиролиза.

Таблица 5.14