МОДЕЛИРОВАНИЕ ПРИСТЕННОЙ ТУРБУЛЕНТНОСТИ

В литературе известно большое число моделей турбулентной вяз­кости. Основные модели, нашедшие практическое применение в расче­тах трения и теплообмена [9, 21, 22, 34], можно разделить на полуэм­пирические с замыканием на уровне уравнений Рейнольдса (табл. 5.3) и многопараметрические с замыканием уравнений Рейнольдса с по­мощью дополнительных дифференциальных уравнений.

Сравнение результатов расчета конвективного теплообмена по моде­лям на основе интегральных соотношений B.C. Авдуевского, интеграль­ной теории С.С. Кутателадзе — А.И. Леонтьева и на основе полной теории пограничного слоя с результатами расчета по алгебраической и энерге­тической моделям турбулентности выполнено применительно к данным экспериментов с соплом Лаваля, приведенным на рис. 5.5 (программы В.Г. Зубкова, В.А. Стрелкова, В.П. Осипова).

Рабочим телом служил сухой очищенный воздух, значения коэффи­циентов теплообмена на гладкой непроницаемой стенке определены методом обращения теплового потока (съем тепла с тонкой пермал-лоевой ленты, нагреваемой электрическим током). В расчетах по всем моделям были использованы опытные значения давления и температур­ного фактора по длине сопла.

Лучшим совпадением с экспериментом обладают модели на основе Интегральных соотношений B.C. Авдуевского и интегральной теории С.С. Кутателадзе - А.И. Леонтьева.

Наличие возмущающих факторов (вдув и шероховатость) корректно учитывают модели интегральной теории при небольших затратах вре­мени, и именно такие модели следует использовать при проектировании тепловой защиты РДТТ. Однако в ряде случаев при действии других возмущающих факторов (неравновесное горение в пограничном слое, переходные явления и др.) необходимо применение моделей на основе полной теории. Характерным примером является явление ламинаризации турбулентного пограничного слоя, т.е. обратный переход к слоисто­му течению [23], при этом получено снижение уровня теплообмена в два раза по сравнению с рассчитанным по интегральной теории турбу­лентного пограничного слоя.

В экспериментах с соплом перед цилиндрической горловиной также наступило это явление (см. рис. 5.4). Наступление ламинаризации опре­деляет критическое значение параметра ускорения

.

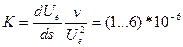Только модели на основе полной теории пограничного слоя с энергетической гипотезой о турбулентности позволяют предсказывать эффект ламинаризации. Результаты математического моделирования конвектив­ного теплообмена для условий экспериментов в сопле позволили уста­новить, что участок ламинаризации имел протяженность около 6 мм вверх по потоку от начала цилиндрической горловины (в эксперимен­тах только одна точка измерения оказалась на участке ламинаризации).

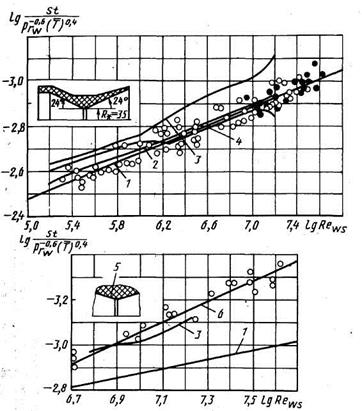
Рис. 5.5. Сравнение результатов расчета конвективного теплообмена по различным моделям:

1 — модель B.C. Авдуевского; 2 - интегральная теория пограничного слоя; 3 - полная теория пограничного слоя, энергетическая модель турбулентности; 4 - полнаятеория пограничного слоя, модель пути смешения; 5 — точка измерения теплообмена на участке ламинаризации; 6 - St~Re 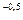; о - экспериментальные данные дозвуковой участок сопла; • - экспериментальные данные, сверхзвуковой участок сопла.

Явление ламинаризации имеет сложную физическую природу, и пользоваться эмпирическими формулами для расчета теплообмена типа зависимости Моретти и Кейса

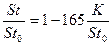(5.7)

следует осторожно. Так, эксперименты в сопле, показанном на рис. 5.5,
не подтверждают расчеты по (5.7), а параметр 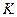не содержит характерис­тик пограничного слоя.