НЕСТАЦИОНАРНЫЙ ТЕПЛООБМЕН В РДТТ
В общем случае существует взаимодействие теплового пограничного слоя газа с температурным полем обтекаемого тела, и задача определения теплообмена и трения должна решаться сопряженной. Согласно А.В. Лыкову критерием сопряженности внешней и внутренней задач теплообмена служит величина, пропорциональная отношению термических сопротивлений теплового пограничного слоя газа и твердого тела, называемая критерием Брюна.
Применительно кобтеканию пластины толщиной 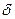 критерий Брюна определен выражением
критерий Брюна определен выражением
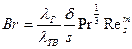 ,
,
где т — 0,5 для ламинарного режима течения и m = 0,2 для турбулентного.
Если с точностью до 1% Вг>0,02, то задачу необходимо решать всопряженной постановке, и понятие коэффициента теплообмена исчезает.
Протекание химических реакций в пограничном слое и на стенке резко усложняет сопряженную задачу. Для угле- и стеклопластиков тепловой защиты тракта сопла РДТТ при Res<1•107 значения критерия Брюна позволяют не решать сопряженную задачу, и в ряде случаев традиционная концепция коэффициента теплообмена вполне применима. Эти материалы характеризуются незначительным изменением температуры стенки во времени после быстрого выхода на установившееся значение вследствие низких значений теплопроводности.
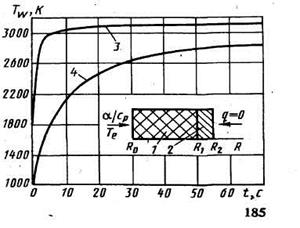
Применение пирографитов и углерод-углеродных композиций в качестве материалов тепловой защиты тракта приводит к значениям критерия Брюна еще меньше ввиду больших значений теплопроводности.Но это вызывает значительное изменение температуры стенки во времени. Расчетное изменение температуры поверхности во времени различных материалов для одного сечения сопла приведено на рис. 5.14.
Нестационарность значения Tw, особенно в начальные моменты времени, может привести к интенсификации теплообмена по сравнению со случаем Tw=const в одинаковых условиях обтекания. Относительнаяошибка в определении числа Стантона без учета влияния нестационарности температуры стенки может составлять 15% при значениях 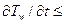 2800К/с (по данным А.В. Фафурина). Для инженерных расчетов такой погрешностью можно пренебречь и не решать сопряженную задачу.
2800К/с (по данным А.В. Фафурина). Для инженерных расчетов такой погрешностью можно пренебречь и не решать сопряженную задачу.
|
Рис. 5.14. Температура стенки материалов тепловой защиты во времени:
1 – тепловая защита; 2 – конструкция; 3 – расчет для углепластика; 4 – расчет для УУКМ.
Расчетные методы, основанные на применении коэффициента теплообмена, согласно В.К. Кошкину требуют коррекции рассчитанных значений 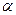 в стационарных условиях с помощью поправочных множителей. При
в стационарных условиях с помощью поправочных множителей. При
турбулентном режиме течения конвективный теплообмен зависит oт
значения первой производной температуры стенки по времени, а не
от закона изменения Tw(t). В РДТТ обычно 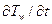 >0 и значение
>0 и значение
поправочного множителя можно вычислять по формуле
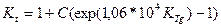 ; (5.10)
; (5.10)
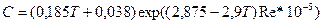 ;
;
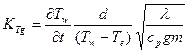 ,
,
где d — диаметр канала; m — расход газа; (Tw-Te)0 — перепад температур в установившихся условиях.
Зависимость (5.10) справедлива при KTg=0...1,6•10 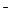 4, Re=8*104...4,5*105.
4, Re=8*104...4,5*105.
При строгом анализе Tw{t) (скалывание чешуек прококсованного слоя вследствие термических и усадочных напряжений может привести к осцилляции температуры стенки во времени, период спада давления) значения Кт 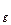 в отдельные моменты времени будут меньше нуля. В этом: случае
в отдельные моменты времени будут меньше нуля. В этом: случае
Kt=1-(1,41Т-0,97)(1-exp(AKТg);
A=793 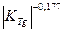 ;
; 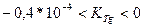 ;
;
A=1,47 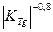 ;
; 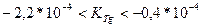 .
.
При уменьшении температуры стенки вниз по потоку, характерном для сопла РДТТ, возможно появление в отдельных сечениях отрицательных значений коэффициента теплообмена, а числа Стантона при переменных и постоянных условиях на границе могут сильно отличаться.
В ряде случаев ошибка в определении числа Стантона при переменной по длине температуре стенки будет значительной. Согласно А.Ш. Дорфману относительная ошибка в значении числа Стантона вследствие, не учета роли условий на стенке будет порядка
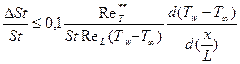 ,
,
где L — характерный размер обтекаемого тела; ( 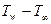 ) - температурный напор, определенный как разность между температурой стенки и температурой ядра потока T
) - температурный напор, определенный как разность между температурой стенки и температурой ядра потока T 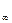 (для случая сжимаемого газа значение T
(для случая сжимаемого газа значение T 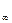 принимают равным температуре торможения).
принимают равным температуре торможения).
Ошибка в значении St увеличивается по мере роста отношения производной температурного напора к значению температурного напора. Консервативность теплообмена восстанавливают в некоторой степени путем замены T 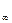 значением температуры восстановления на адиабатической стенке Те.
значением температуры восстановления на адиабатической стенке Те.
При обтекании элементов устройств создания управляющих усилий РДТТ накладывается еще и внешняя нестационарность — изменение во времени расхода и температуры рабочего тела. При исследовании нестационарного теплообмена в трубах при переменном расходе газа В.К. Кошкиным установлены эмпирические зависимости поправочного множителя к значениям коэффициентов теплообмена:
при увеличении расхода и температуры стенки
К=1+0,1155 (КТ)0,353(0,0213+0,000415КT)/ 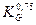 ,
,
КТ =0...25, KG=0...15;
при уменьшении расхода и температуры стенки
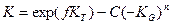 ;
;
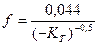 ;
; 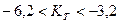 ;
;
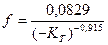 ;
; 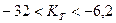 ;
;
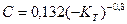 и
и 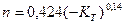 ;
; 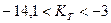 ;
;
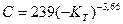 и
и 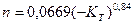 ;
; 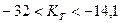 ;;
;;
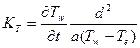 ;
;
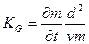 ;.
;.
В экспериментах величины КТ и Т не были независимыми, и влияние температурного фактора на теплообмен не установлено. В явном виде отсутствует и влияние числа Рейнольдса.
Полученные данные указывают на существенное отличие теплообмена при изменении расхода от уровня, рассчитанного в предположении о квазистационарности процессов течения и теплообмена. При умеренныx значениях | 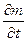 | в случае
| в случае 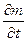 >0 тепловые потоки возрастают, а в случае
>0 тепловые потоки возрастают, а в случае 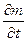 <0 — уменьшаются. Для больших значений |
<0 — уменьшаются. Для больших значений | 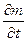 | возможно наступление ламинаризации при
| возможно наступление ламинаризации при 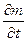 >0, апри
>0, апри 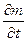 < 0 может произойти увеличение уровня теплообмена.
< 0 может произойти увеличение уровня теплообмена.
Нестационарный теплообмен при переменной температуре газа исследован А.В. Фафуриным. Если 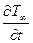 < 0, то происходит увеличение уровня теплообмена. Опытные данные аппроксимированы эмпирической зависимостью
< 0, то происходит увеличение уровня теплообмена. Опытные данные аппроксимированы эмпирической зависимостью
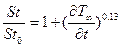
в диапазоне чисел Re 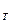 **=100...2000 и
**=100...2000 и 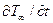 =0...400.
=0...400.
Наибольшее влияние на отличие от уровня теплообмена, рассчитанного для квазистационарных условий, оказывают факторы внешней нестационарности 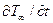 ;
; 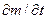 ,а влияние внутренней нестационарности
,а влияние внутренней нестационарности 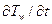 существенно меньше.
существенно меньше.
Корректный расчет теплового состояния многослойной составной конструкции сопла РДТТ требует решения сопряженной задачи, позволяющей учесть изменение температуры стенки по контуру (как вследствие изменения уровни теплообмена, так и смены материалов на участках тракта), большие значения 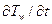 в начальные моменты времени и изменение режима работы двигателя.
в начальные моменты времени и изменение режима работы двигателя.
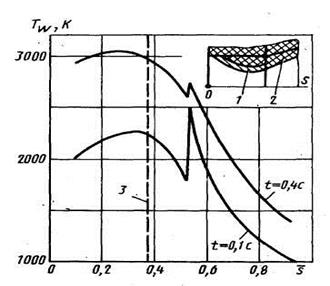
Существенным в упрощении задачи является подход, заключающийся в использовании стационарных уравнений пограничного слоя и одномерного уравнения нестационарной теплопроводности с последующей итерацией решений для выбранных моментов времени. Для случая течения сжимаемого газа в канале сложной формы с составными многослойными стенками значения температуры поверхности приведены на рис. 5.15 согласно данным Б.Б. Петрикевича.
|
Рис. 5.15. Распределение температуры -стенки по длине канала:
1 - вольфрам; 2 - углепластик; 3 - минимальное сечение
В начальные моменты времени имеется существенный разрыв в значениях Tw(s) настыке материалов с различной теплопроводностью, что приводит к деформации пограничного слоя.
Дата добавления: 2016-06-29; просмотров: 2359;











