ТЕЧЕНИЕ ГАЗА В КАНАЛАХ НЕЦИЛИНДРИЧЕСКИХ ФОРМ

Поперечное сечение РДТТ, свободное для прохода газов, может быть разнообразным, по форме (круглым, звездообразным и др.) и иметь площадь, переменную по длине двигателя. Газовый тракт в камере с за­рядом нецилиндрической формы с резкими изменениями F целесооб­разно представить в виде нескольких цилиндрических участков (с по­стоянной на каждом участке площадью проходного сечения) и местных сопротивлений на стыках этих участков (с резким изменением площади проходного сечения). В этих случаях газодинамический расчет РДТТ про­водится последовательно по выделенным участкам в направлении от сопла к переднему дну, так как параметры критического сечения явля­ются определяющими граничными условиями.

Щелевой заряд: толстосводная трубчатая шашка с продольными пропилами, относительная длина которых порядка примерно 0,3. Ее можно представить в виде двух участков с постоянными площадями про­ходных сечений (щелевая часть и часть с круглым каналом) и внезап­ным сжатием (если щели обращены к переднему дну) или внезапным расширением (если щели обращены к сопловой крышке). В случае ще­левого заряда имеем (сечения 1—1 и 2—2 проходят вблизи внезапного из­менения площади проходного сечения)

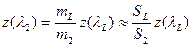
и

,

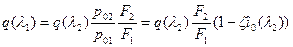где коэффициент местных потерь

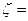
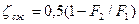- щели обращены к переднему дну;

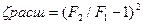- щели обращены к сопловой крышке;

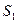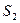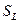, и — площади горящих поверхностей на участках от х = 0 до се­чений 1—1, 2—2 и L—L соответственно.

Распределение скоростей газового потока в канале с внезапным рас­ширением потока определяется системой уравнений неразрывности и ко­личества движения:

;

.

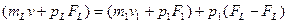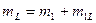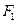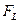Здесь и — площади проходных сечений узкой и широкой час­тей канала соответственно; т 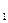и m_L — количество газа, проходящее че­рез эти сечения; m_1L.— количество газа, выделяемое с поверхности го­рения S_1L на участке между сечениями 1-1 и L-L.

С помощью газодинамических функци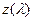й и 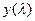уравнение пол­ного импульса можно представить в виде

,

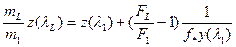при этом

.

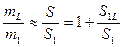Результаты расчета 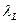в зависимости от 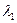приведены в табл. 3.5 при 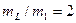, 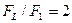и к =1,25. При известном 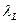приведенная ско­рость на выходе из узкой части канала 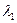определяется графически как корень трансцендентного уравнения. Коэффициент восстановления пол­ного давления в широкой части канала определяется по уравнению не­разрывности

.

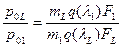Значение коэффициента восстановления полного давления по всему каналу определяется соотношением (см. табл. 3.5)

.

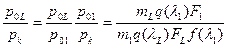Из данных, приведенных в табл. 3.5, видно, что повышение плотнос­ти заряжания из-за уменьшения площади проходного сечения канала в передней части приводит к увеличению потерь полного давления. Напри­мер, при 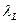=0,45 коэффициент восстановления полного давления в ступенчатом канале, где F_L/F₁=2, равен 0,84, а в цилиндрическом ка­нале (F=F_L=const) — 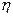=0,91. Увеличение плотности заряжания путем уменьшения площади проходного сечения по всему каналу до величины

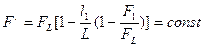
(где ;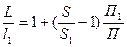

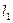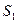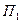, , - длина, площадь горящей поверхности и периметр сечения уз­кой части ступенчатого канала) приводит к существенному увеличению скорости на выходе из канала и, следовательно, к увеличению эрозион­ного горения и потерь полного давления. Например, 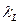=0,48 вместо 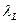=0,32 в ступенчатом канале.

Таблица 3.5