ТЕЧЕНИЕ ГАЗА В ЦИЛИНДРИЧЕСКОМ КАНАЛЕ

Установившееся течение продуктов сгорания в цилиндрическом ка­нале с подводом массы определяется системой уравнений:

;

;

;

,

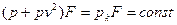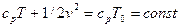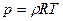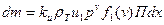где П — периметр горящего контура*

Если ввести газодинамические функции, то получим

;

; ;

.

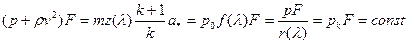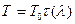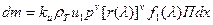Граничные условия таковы:

При х = 0 ;

При х=L .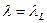

Значение 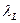на выходе канала определяется по уравнению неразрыв­ности (см. п. 3.2.1).

На донном конце заряда (х = 0)

Р=Ро=Р_к; Т = Т₀;

p=Po=P_K/(RT₀).

Из первого уравнения исходной "системы и граничного условия (х = 0) следует ряд соотношений, связывающий параметры потока в сечении, характеризуемом приведенной скоростью 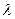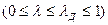, с давлением р_к и температурой Т_о в донной части двигателя:

; ;

; ;

.

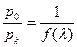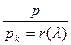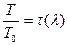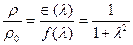В частности, из этих уравнений следует, что перепад давлений по всей длине заряда 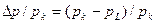и коэффициент восстановления пол­ного давления в канале 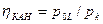(а также изменение других газоди­намических характеристик) не зависят от распределения массоприхода по длине канала и равны (см. табл. 3.3):

; .

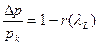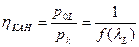Рассеяние полной энергии в канале обусловлено смешением двух потоков, имеющих различные скорости в осевом направлении: основного
течения 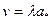и притока газа от горящей поверхности со скоростью
.

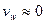Из уравнения неразрывности получаем

.

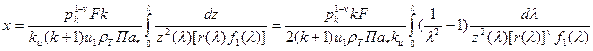Неопределенность по р_к устраняется с помощью граничного условия на сопловом конце заряда х =L, :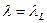

,

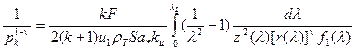где S=ПL.

Запишем соотношение для р_к в обычном виде

,

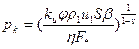где 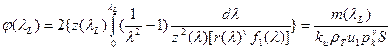- коэффициент средней по каналу скорости горения;

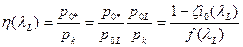— коэффициент восстановления полного давления в двигателе (см. табл. 3.3).

В первом приближении скорость горения одинакова по всему кана­Лу 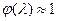; . При этом имеем

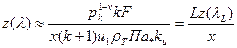
или ,

приблизительно

.

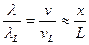Эти приближенные зависимости могут быть использованы для последу­ющего расчета изменения скорости горения по длине канала вследствие падения статического давления 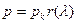и увеличения эрозионной соствляющей 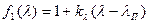(см. п. 2.3.5).

Коэффициент 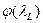средней по поверхности скорости горения твер­дого топлива обычно больше единицы при 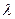> 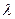_п. Он рассчитывается ме­тодом численного интегрирования при заданной зависимости f 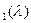(табл. 3.4 для топлива JPN).

Таблица 3.4