Учет влияния конечного числа лопаток на напор насоса

При рассмотрении движения жидкости в межлопаточном канале считалось, что движение струйное и скорости распределены равномерно по сечению канала и, как следствие, давление жидкости по обе стороны лопатки одинаково. Вместе с тем приращение энергии жидкости возможно только в том случае, если давление на переднюю стенку лопатки больше, чем на заднюю. Рассмотрим этот вопрос исходя их вихревой теории движения жидкости. Предварительно рассмотрим такой пример. Пусть имеем цилиндрический сосуд, наполненный жидкостью (рис. 10). 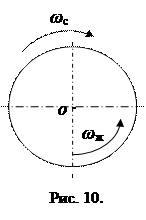Если этот сосуд привести во вращательное движение вокруг неподвижной оси о с угловой скоростью ω_с, то жидкость, стремясь сохранить состояние покоя, будет как бы поворачиваться относительно этого сосуда с угловой скоростью ω_ж. Аналогичная картина будет наблюдаться с жидкостью, расположенной в межлопаточном канале рабочего колеса с конечным числом лопаток, который будет закрыт на входе и выходе. Рассоложенная между лопатками жидкость, как и в предыдущем примере, стремясь сохранить состояние покоя, будет вращаться в межлопаточном канале в противоположном направлении вращению колеса. Если же открыть вход и выход меж-

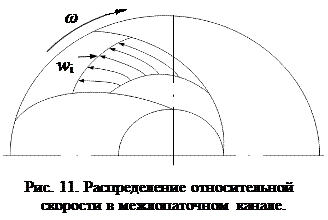лопаточного канала, то на вращательное движение жидкости будет накладываться поступательное движение и результирующая скорость движения жидкости в межлопаточном канале w_i будет распределена не равномерно: у вогнутой части лопатки она будет больше, а у выпуклой – меньше (рис. 11). Как следствие, давление жидкости на лопатку с выпуклой её стороны будет больше, а с вогнутой меньше. План скоростей при конечном числе лопаток изменится по сравнению с исходным и примет вид, приведенный на рис. 12.

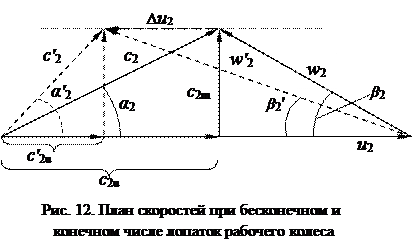Из приведенного рисунка видно, что при конечном числе лопаток происходит уменьшение окружной составляющей абсолютной скорости c_2u на величину Δu₂, изменяется угол β , меняются по величине и направлению векторы абсолютной с₂ и относительной скорости w₂. Однако на самом деле конструктив-ные углы лопаток остаются неизменными и жидкость вынуждена двигаться согласно профилю лопатки, теряя при этом часть переданной ей энергии. На характер распределения скорости в межлопаточном канале существенное влияние оказывает вязкость жидкости.

Для учета влияния конечного числа лопаток на напор насоса предложено вводить в уравнение Эйлера поправочный коэффициент к₁, равный отношению окружной составляющей абсолютной скорости c'_2u при конечном числе лопаток, к окружной составляющей абсолютной скорости c_2u при бесконечном числе лопаток: к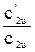₁= < 1.

У большинства современных насосов к₁=0,8.

Для вычисления коэффициента к₁ предложен ряд формул, например формула Г.Ф. Проскуры:

к₁= 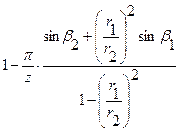, (14)

где z – число лопаток рабочего колеса.

Более простая формула для вычисления коэффициента к₁ предложена Стодолой:

к₁= 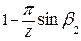. (15)

Оптимальное число лопаток предлагается вычислять по формуле:

z= 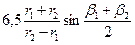. (16)

Уравнение Эйлера с учетом конечного числа лопаток (при радиальном входе жидкости) примет вид:

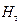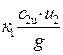= . (17)