Последовательное соединение резистивного и емкостного элементов
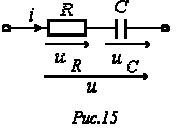 Опуская промежуточные выкладки, с использованием соотношений (2) и (4) для ветви на рис. 15 можно записать
Опуская промежуточные выкладки, с использованием соотношений (2) и (4) для ветви на рис. 15 можно записать
. 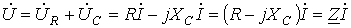 , ,
| (8) |
где
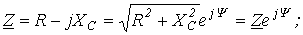
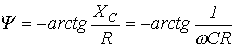 , причем пределы изменения
, причем пределы изменения 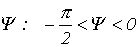 .
.
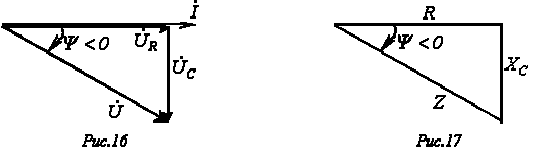
|
На основании уравнения (7) могут быть построены треугольники напряжений (см. рис. 16) и сопротивлений (см. рис. 17), которые являются подобными.
Параллельное соединение резистивного и емкостного элементов
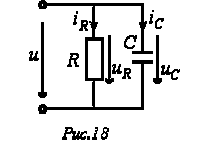
Для цепи на рис. 18 имеют место соотношения:
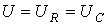 ;
;
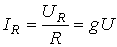 , где
, где 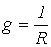 [См] – активная проводимость;
[См] – активная проводимость;
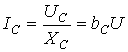 , где
, где 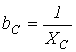 [См] – реактивная проводимость конденсатора.
[См] – реактивная проводимость конденсатора.
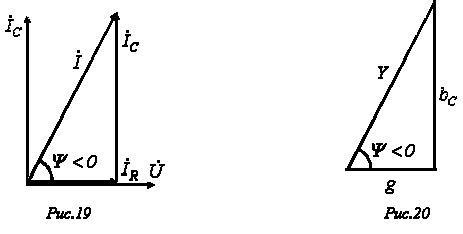
|
Векторная диаграмма токов для данной цепи, называемая треугольником токов, приведена на рис. 19. Ей соответствует уравнение в комплексной форме
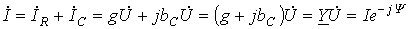 ,
,
где 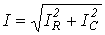 ;
;
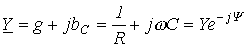 - комплексная проводимость;
- комплексная проводимость;
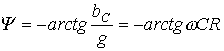 .
.
Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 20.
Для комплексного сопротивления цепи на рис. 18 можно записать
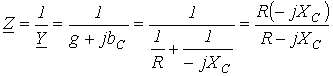 .
.
Необходимо отметить, что полученный результат аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.
Дата добавления: 2016-06-29; просмотров: 1787;











