Частотные свойства p-n-перехода

Будем считать, что к р-n-переходу кроме постоянного прямого напряжения U приложено синусоидальное напряжение с малой амплитудой U_m и частотой w. Частотные свойства p-n-перехода можно характеризовать зависимостью от часто­ты отношения амплитуд тока и напряжения, т.е. комплексной проводимостью 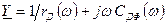. Для расчета проводимости формально можно использовать эк­вивалентную схему (линейную модель), приведенную на рис. 3.23,б, если уже из­вестны частотные зависимости величин ее элементов. Мы уже отмечали, что барьерная емкость от частоты не зависит, а диффузионная емкость убывает с повышением частоты. О частотной зависимости дифференциального сопротив­ления речи вообще не было.

Достаточно строгое решение задачи без привлечения модели о частотной зависимости диффузионной емкости и дифференциального сопротивления проводится на основе фундаментального уравнения полупроводниковой электроники – уравне­ния непрерывности (см. § 2.2.3).

При рассматриваемом прямом включении р-n-перехода предполагается, что в ем­кости С_д преобладает диффузионная емкость, так что 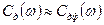, а проводимость

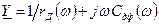(3.63)

Приведем без расчета результаты, полученные для p-n-перехода с размера­ми областей, много большими соответствующих диффузионных длин носителей 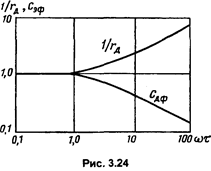заряда. На низких частотах диффе­ренциальное сопротивление r_Д име­ет такое же значение, так и R_диф, оп­ределенное по ВАХ. Значение диф­фузионной емкости оказывается в 2 раза меньше, чем определенное по формуле (3.61). На высоких частотах дифференциальное сопротивление r_Д убывает примерно обратно про­порционально 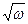(как и диффузион­ная емкость), а проводимость 1/r_Д соответственно растет.

За критерий «низкой» частоты бе­рутся значения от wt_p<< 1 и wt_n <<1, где t_p и t_n – времена жизни неосновных носителей в областях. За критерий «высокой» частоты берутся значения wt_p>>1 и wt_n>>1.

На рис. 3.24 показаны зависимости дифференциальной проводимости и диффузионной емкости от нормализованной частоты, при этом для упрощения предполагался асимметричный переход. Значения величин нормированы к низкочастотным значениям 1/R_диф и С_{дф о} [4].