Параметры и модель р-n-перехода в динамическом режиме

3.6.1. Дифференциальное сопротивление

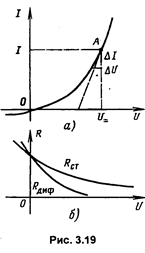
Оно определяется выражением R_диф = dU/dI и характеризует крутизну ВАХ (рис. 3.19,а) в рассматриваемой точке (R_диф обратно пропорциональна производной dI/dU). Для идеализированного пе­рехода по формуле (3.40) можно получить аналитическое выраже­ние

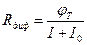(3.51)

Для прямой ветви ВАХ, где I >>I₀,

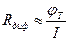(3.51 a)

При комнатной температуре j_T = 0,026 В. Выразив I в миллиамперах, получим ши­роко используемую для оценок формулу

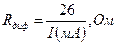(3.52)

При прямом напряжении R_диф мало и убывает с ро­стом напряжения, а при обратном очень велико. Дифференциальное со­противление называют также сопро­тивлением переменному току.

3.6.2. Барьерная емкость

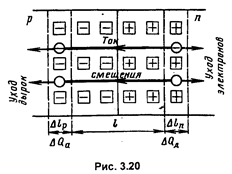Обедненный слой перехода подобен конденсатору, так как в нем «связаны» равные по величине, но противоположные по зна­ку заряды ионов акцепторов Q_a и доноров Q_д (|Q_a| = Q_д). Так как эти заряды определяют потенциальный барьер, то и емкость на­зывается барьерной.

По определению ток смещения I_см =ee₀ дЕ/дt = дQ/дt. Это соот­ношение можно записать в виде

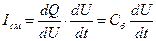(3.53)

где

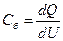(3.54)

называется дифференциальной барьерной емкостью р-п-перехода.

Если приращение напряжения мало, то изменения толщины слоя DI_р и DI_n малы. Следовательно, можно считать, что переход эк­вивалентен конденсатору, «обкладками» которого являются тонкие слои DI_р и DI_n, находящиеся на расстоянии, равном исходной толщи­не обедненного слоя I (DI_р << I, DI_n << I). Приращение заряда DQ про­исходит на этих «обкладках», так как между ними нет изменения за­рядов. Общая формула для барьерной ем­кости как емкости плоского конденсатора:

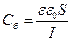(3.55)

Подставив в (3.55) толщину перехода I из формулы (3.15) и про­изведя преобразования, получим зависимость С_б от напряжения и других параметров для резкого р-n-перехода:

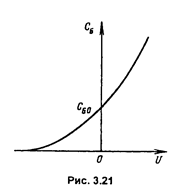
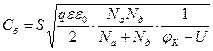(3.56)

Зависимость С_б от напряжения (вольт-фарадная характеристика) показана на рис. 3.21. Значение барьерной емкости пои U = 0

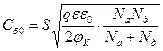(3.57)

Используя (3.57), можно переписать (3.56) в более простом виде:

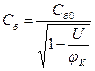(3.58)

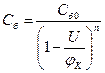
3.6.3. Диффузионная емкость

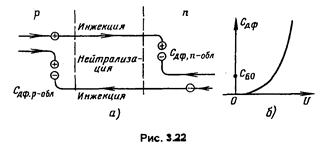Эта емкость связана с наличием в р- и n-областях избыточных носителей. На рис. 2.8 было показано распределение неравновес­ных и избыточных неосновных и основных носителей в областях. При прямом напряжении происходит процесс инжекции неосновных носителей (рис. 3.22,а). Появляются избыточные концентрации не­основных носителей в каждой области и в соответствии с условием электрической нейтральности равные им избыточные концентрации основных носителей. Таким образом, в n-области (как и в конденса­торе) оказываются в равном количестве положительный заряд из­быточных дырок (неосновные носители) и отрицательный заряд из­быточных электронов (основные носители). Аналогично р-область ведет себя как конденсатор с отрицательным зарядом избыточных электронов (неосновные носители) и равным ему положительным зарядом избыточных дырок (основные носители).

Процесс накопления избыточных зарядов – инерционный про­цесс, связанный с временем жизни неосновных носителей. Это нако­пление принято характеризовать дифференциальной диффузионной емкостью, которая учитывает изменение избыточных носителей (дырок и электронов) в обеих областях при изменении напряжения:

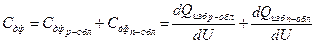(3.60)

Используя формулы (3.35) для распределения избыточных но­сителей вне перехода и формулы (3.60) и (3.7), получаем

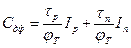(3.61)

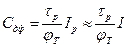(3.61а)

Но для идеализированного р-n-перехода j_Т/I – дифференциаль­ное сопротивление R_диф (3.51 а), поэтому

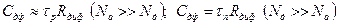(3.62)

Через барьерную емкость протекают токи смещения, в то время как через диффузионную емкость – ток носителей. Диффузи­онная емкость отражает инерционность процесса накопления и рас­сасывания избыточных носителей в областях р-n-структуры. Поэто­му диффузионную емкость называют иногда «фиктивной» емко­стью, формально позволяющей описать инерционные свойства р-n-перехода. При этом также говорят о зарядке и разрядке этой емкости, как для обычного конденсатора.

3.6.4. Малосигнальная модель p-n-перехода

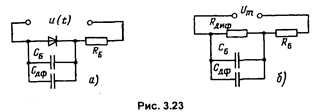На рис. 3.23,а изображена нелинейная электрическая модель (или эквивалентная схема) p-n-перехода, содержащая безинерци­онный диод (или зависимый генератор тока), ВАХ которого предста­вляется уравнением (3.43), параллельно включенные емкости С_б и С_дф, также зависящие от напряжения.

Модель называется линейной, если к р-n-переходу прикладыва­ется переменное синусоидальное напряжение малой амплитуды (малый сигнал). Линейная модель (рис. 3.23,б) отличается от нели­нейной тем, что вместо идеализированного p-n-перехода включено дифференциальное сопротивление R_диф, представляющее собой сопротивление перехода на переменном токе.