Метод расчета концентраций
Концентрация электронов n в зоне проводимости и концентрация дырок р в валентной зоне могут быть представлены следующими общими выражениями:
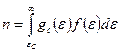 ; (2.1)
; (2.1)
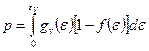 ; (2.2)
; (2.2)
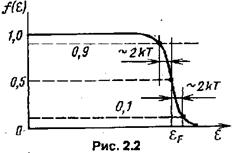
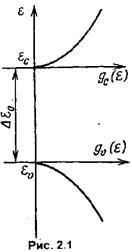 Величины
Величины 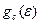 и
и 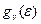 – плотности квантовых состояний, Функция
– плотности квантовых состояний, Функция 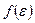 в (2.1) есть вероятность того, что состояние с энергией
в (2.1) есть вероятность того, что состояние с энергией 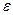 занято электроном. Соответственно
занято электроном. Соответственно 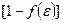 означает вероятность отсутствия электрона на уровне в валентной зоне, т.е. вероятность существования дырки.
означает вероятность отсутствия электрона на уровне в валентной зоне, т.е. вероятность существования дырки.
При квантово-механическом рассмотрении установлено, что
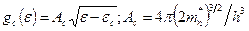 (2.3)
(2.3)
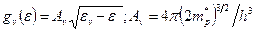 (2.4)
(2.4)
где h – постоянная Планка; 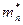 и
и 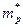 – эффективные массы электронов и дырок.
– эффективные массы электронов и дырок.
Вероятностная функция f(e) в (2.1) и (2.2) определяется по формуле
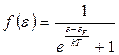 (2.5)
(2.5)
которая называется функцией распределения Ферми-Дирака. В этой функции k – постоянная Больцмана, Т – абсолютная температура, а 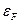 – энергия уровня Ферми. Очевидно, что при
– энергия уровня Ферми. Очевидно, что при 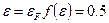 . Поэтому формально уровнем Ферми является уровень, вероятность нахождения электрона на котором равна 0,5 (рис. 2.2). При Т > 0 К функция имеет плавный, но быстрый спад приблизительно в интервале значений энергии ±2 kT около уровня
. Поэтому формально уровнем Ферми является уровень, вероятность нахождения электрона на котором равна 0,5 (рис. 2.2). При Т > 0 К функция имеет плавный, но быстрый спад приблизительно в интервале значений энергии ±2 kT около уровня 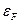 . При комнатной температуре (T=300 К) kT= 0,026 эВ, т.е. ±2kT= ±0,052 эВ, что значительно меньше
. При комнатной температуре (T=300 К) kT= 0,026 эВ, т.е. ±2kT= ±0,052 эВ, что значительно меньше 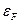 , составляющего единицы электронвольта. Вероятность
, составляющего единицы электронвольта. Вероятность  при
при 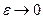 , и
, и  при
при 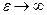 .
.
Функцию распределения 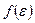 необходимо «привязывать» к зонной диаграмме полупроводника. Как правило, для этого надо знать, где находится уровень Ферми. У обычно используемых полупроводников
необходимо «привязывать» к зонной диаграмме полупроводника. Как правило, для этого надо знать, где находится уровень Ферми. У обычно используемых полупроводников 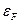 находится в запрещенной зоне: в n-полупроводнике – на «расстоянии»
находится в запрещенной зоне: в n-полупроводнике – на «расстоянии» 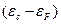 >>2kT от дна зоны проводимости, а в р-полупроводнике – на расстоянии
>>2kT от дна зоны проводимости, а в р-полупроводнике – на расстоянии  >> 2kTот потолка валентной зоны и в формуле (2.5) можно пренебречь в знаменателе единицей, т.е. функция распределения Ферми-Дирака сводится приближенно к функции распределения Максвелла-Больцмана:
>> 2kTот потолка валентной зоны и в формуле (2.5) можно пренебречь в знаменателе единицей, т.е. функция распределения Ферми-Дирака сводится приближенно к функции распределения Максвелла-Больцмана:
 (2.6)
(2.6)
Полупроводники, для которых справедлива функция распределения Максвелла- Больцмана, называют невырожденными. Для них характерно то, что число частиц значительно меньше числа разрешенных состояний. Если в полупроводнике уровень Ферми доказывается в интервале 2kT вблизи границ зон или внутри этих зон, то следует пользоваться только функцией распределения Ферми-Дирака, а состояние полупроводника становится вырожденным.
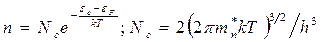 (2.7)
(2.7)
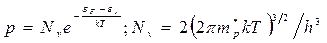 (2.8)
(2.8)
Формулы (2.7) и (2.8) являются универсальными, так как применимы для расчета концентраций в любых типах полупроводников: собственном (типа i) и примесных (типов п и р). Коэффициенты 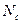 и
и  следует трактовать как эффективное число состояний, расположенных на границах зон (уровней
следует трактовать как эффективное число состояний, расположенных на границах зон (уровней 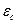 и
и  , которые только и входят в формулы). Значения
, которые только и входят в формулы). Значения 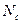 и
и  для кремния и германия составляют примерно 1019 см-3.
для кремния и германия составляют примерно 1019 см-3.
Формулы (2.7) и (2.8) следует также понимать как отражение взаимосвязи между концентрацией (числом носителей) и уровнем Ферми. Если известно значение 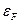 , то можно вычислить концентрации п и р,соответствующие этому значению
, то можно вычислить концентрации п и р,соответствующие этому значению 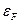 . Если же известна концентрация п (или р), то можно вычислить соответствующее ей значение
. Если же известна концентрация п (или р), то можно вычислить соответствующее ей значение 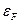 . Формула для
. Формула для 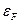 в этом случае получается из (2.7) или (2.8), но значение в результате расчета, естественно, должно получиться одинаковым:
в этом случае получается из (2.7) или (2.8), но значение в результате расчета, естественно, должно получиться одинаковым:
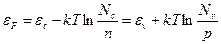 (2.9)
(2.9)
Одинаковый результат является следствием имеющейся связи между значениями концентраций п и р, т.е. связи между полным числом носителей в зоне проводимости и валентной зоне. Рассмотрим эту связь.
Используя (2.7) и (2.8), найдем произведение концентраций:

Так как ширина запрещенной зоны 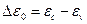
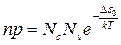 (2.10)
(2.10)
Применим (2.10) для собственного (чистого, беспримесного) полупроводника, в котором концентрация электронов и дырок одинакова  . Получим формулу
. Получим формулу
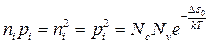 (2.11)
(2.11)
которую можно использовать для расчета концентраций носителей в собственном полупроводнике, не зная положения уровня Ферми:
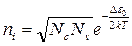 (2.12)
(2.12)
или преобразования формулы (2.10) до вида
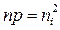 (2.13)
(2.13)
Смысл этого соотношения состоит в том, что увеличение концентрации частиц с одним знаком заряда сопровождается уменьшением концентрации частиц с другим знаком. Такая зависимость объясняется тем, что при увеличении, например, концентрации электронов п обязательно пропорционально увеличится и вероятность рекомбинации носителей, в результате чего будет пропорционально убывать концентрация дырок р.
Расчет по формуле (2.12) дает следующие значения 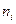 : для Ge – 2,4 1013 см-3; для Si – 1,45 1010 см-3 ; для GaAs – 1,79 106 см-3. Превышение ширины запрещенной зоны кремния по сравнению с германием всего в 1,12/0,66=1,7 раза привело к уменьшению концентрации собственных носителей приблизительно в 103 раз.
: для Ge – 2,4 1013 см-3; для Si – 1,45 1010 см-3 ; для GaAs – 1,79 106 см-3. Превышение ширины запрещенной зоны кремния по сравнению с германием всего в 1,12/0,66=1,7 раза привело к уменьшению концентрации собственных носителей приблизительно в 103 раз.
Дата добавления: 2016-06-29; просмотров: 2458;











