Вопрос 2. Влияние св-в с-лов на верность передачи.

2.1. Системы с активной паузой и ортогональными сигналами.

Пример à частотно-манипулированные с-лы ЧМ_н

à фазо-манипулированные с-лы с манипуляцией фазы на 90º, ФМ_н с Δφ = 90º.

b_S = 0;

(5.24)

2.2. С-мы, исп. противоположные с-лы S₀(t) = –S₁(t)

Например à фазоманипулированные с-лы с манипуляцией фазы на 180ºС ФМ_н с Δφ = 180º.

b_S = –1;

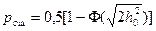(5.25)

– достигается max различие между противополож. с-лами;

– при прочих равных условиях обеспечивают p_ош, min.

2.3 С-мы исп. с-лы с пассивной паузой (энергия затрачивается только на излучение одного из с-лов)

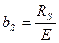
Например à амплитудная манипуляция АМ_н S₀(t) – есть с-л; S₁(t) – нет с-ла.

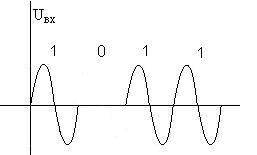
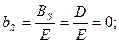
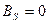, т.к. ВКФ между с-лом и паузой (т.е. ø) – частный случай ортогональных с-лов, но

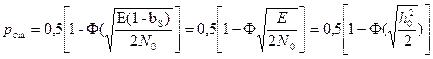
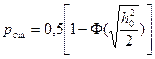(5.26)

Для достижения р_ош, такой же как и для ортогональных с-лов с активной паузой (5.24) необходимо энергию посылки с пассивной паузой увеличить в 2 раза. (Увеличить пиковую мощность посылки и(или) увеличить длительность). И то и др. во многих случаях нежелательно à с-лы с пассивной фазой в современных с-мах цифровой передачи инф. находят ограниченное применение.

2.4. Сравнительный анализ.

Запишем (5.23) в виде

p_ош = 0,5 [1 – Φ(γ_c, h₀)],

где γ_c – постоянный коэф. имеет знак

– для 2.1, (5.24) γ_c = 1

– для 2.2, (5.25) γ_c =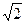

– для 2.3, (5.26) γ_c =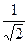

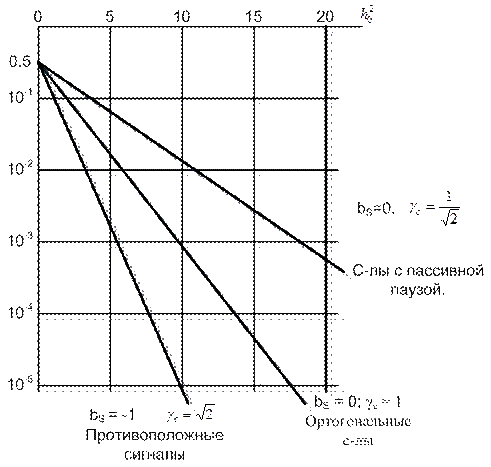
Рис. Зависимость p_ощ от отношения с-ла к помехе для различных классов двоичных с-лов p_ош = f(h₀²)

Сравним (5.24), (5.25) и (5.26), полагая р_ош = const, длит. с-лов = const, а пиковая мощность var. Найдем энергетический выйгрыш при переходе от АМ_н à к ЧМ_н (ФМ_н с Δφ = 90º). Изменение амплитуды колебания (для достижения р_ош без изменения длительности) в 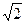раз даст выйгрыш по пиковой нагрузке в 2 раза.

От ЧМ_н à к ФМ_н с Δφ = 180º (противоположные с-лы). Изменение амплитуды колебания (для достижения р_ош без изменения длительности) в 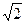раз даст выйгрыш по пиковой нагрузке в 2 раза.

От АМ_н à к ФМ_н с Δφ = 180º. Выйгрыш по пиковой нагрузке в 4 раза.

Определим выйгрыш по средним мощностям

АМ_н P_S = 0,5 P_max.

?