Информационные основы передачи сообщений по каналам связи.

Тема лекции 6. Информационные характеристики источников сообщений и каналов связи.

1. Информационные характеристики источников сообщений.

1.1. Информационные характеристики источников дискретных сообщений.

1.2. Энтропия источников непрерывных сообщений.

2. Информационные описание каналов связи.

	Необходимость изучения вопросов темы 4

При передаче информации необходимо ее каким-то образом численно оценивать.

- Как много надо передать информации?

- Как быстро можно передавать информацию?

- Определить условия согласования в информационном отношении источников и потребителей с каналом.

- Оценить эффективность средств связи и как ее улучшить.

Вопрос 1.

Информация – некоторая совокупность сведений, составляющих меру наших знаний в тех или иных событиях.

à Количество полученной информации равно неопределенности (неопределенность в выборе передаваемого сообщения не от смысла передаваемых сообщений, а от их общего числа).

Интуитивные представления и требования к мере количества информации.

- мера количества информации = 1, для опыта с 1 исходом.

- должна быть пропорциональна количеству равновероятных исходов.

- обладать свойством аддитивности опытов, т.е. информационная сложимость опыта есть сумма информационных составляющих.

- исходам с меньшей вероятностью должно соответствовать большее количество информации.

1.1. Информационные характеристики источников дискретных сообщений.

Пусть источник дискретных сообщений выдает некоторые сообщения, а из ансамбля условились количество информации в этом сообщении определять (4.1)

в основном k = 2 в дальнейшем k – не пишем, а считаем, что k = 2.

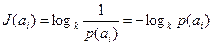(4.1)

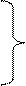Если k = 2 – бит log₂

k = 10 – дит log₁₀

k = e – Мит ln

J (a_i) – не учитывает полезность, ценность или важность сообщений à для математической модели (отказ от учета качества информации) это строгость формулируемых утверждений. Тем более каналы связи сами по себе безразличны к качественным характеристикам передаваемых сообщений.

Качество информации в средствах связи может быть учтено введением категорий и приоритетов сообщений, разных требований к надежности их передачи и т.п.

a₁, a₂, …, a_i, …, a_ma – алфавит источника,

m_a – объем алфавита.

p(a₁), p(a₂), …, p(a_i), …p(a_ma) – вероятности появления символов на выходе источника сообщений.

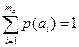
Знание частной информации J(a_i) недостаточно и не всегда необходимо. Для согласования источника сообщений с каналом связи необходимо знать информацион­ные свойства источника сообщений. В целом интересующую характеристику можно рассматривать как мат-ожидание дискретной С.В.

t = сумма произведений значению дискрет. СВ на вероятность

Cлучай 1.

Если символы источника равновероятны и независимы

p(a₁) = p(a₂) = … = p(a_i) = … = p(a_ma) =1/m_a

J(a_i) = log p(a_i) = -log (1/m_a) = log m_a – каждый символ несет одно и тоже количество информации.

Энтропия – среднее количество информации, приходящееся на 1 символ.

H₀(A) = log m_a (4.2)

m_a1 = 2 à H₀ = 1 бит

m_a2 = 8 à H₀ = 3

m_a3 = 32 à H₀ = 5

Как МО случ. дискрет.

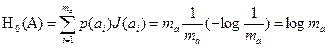
Случай 2

Символы источника неравновероятны и независимы.

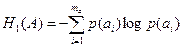(4.3)

«Энтропия» заимствована из термодинамики, где она характеризует аналогичное по форме выражение, характеризующее неопределенность состояния физической системы.

В теории инф – э н т р о п и я характеризует неопределенность ситуации до передачи, т.е. мера неопределенности сообщения.

Пример 4.1

Свойства энтропии.

1. Энтропия есть величина вещественная, ограниченная, неотрицательная.

2. Если опыт имеет один исходный символ H(A) ≥ 0, то Н(А) min n = 0.

3. Энтропия max, если все исходные символы опыта равновероятны.

4. Энтропия опыта с 2-мя исходными может изменяться от 0 до 1.

5. Энтропия возрастает с увеличением числа исходов.

Случай 3

Символы источника неравновероятны и зависимы p(a_l/a_k) – условная вероятность появления символа a_l; вероятность появления символа a_l, при условии, что до этого передавался символ a_k.

J(A_l/a_k) – среднее количество информации, содержащееся в символе a_l, если предыдущим был символ a_k, à частная условная энтропия символа a_l

усреднение по l

J(A_l/a_k)

J(A_l/A_k) = H₂(A) à ср. кол-во инф. в символе a_l (полная условная) энтропия.

усреднение по k

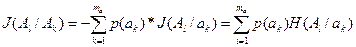
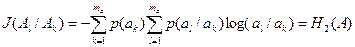(4.4)

По теореме умножения ветвей

p(a_k)p(a_l/a_k)=p(a_k,a_l)

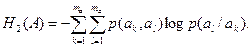
Если источник распространяет 3 символа a_j, a_k, a_l

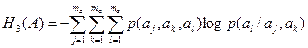
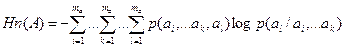(4.5)

Пример 4.2.

Следствия

1. Если символы источника зависимы, то каждый из них несет в среднем меньшее количество инф. по сравнению с независимыми.

2. Уменьшение разницы между условными вероятностями приводит к увеличению энтропии (как и для независимых символов)

p(a1/a1) = p(a2/a2) = 0,2 à 0,469 бит

p(a1/a1) = p(a2/a2) = 0,3 à 0,881 бит

p(a1/a1) = p(a2/a2) = 0,5 à 1,0 бит – значение безусловной энтропии.

3. Условная энтропия изменяется в диапазоне от 0 до значения безусловной энтропии.

4. Условная энтропия уменьшается с увеличением числа символов, между которыми существует статическая взаимосвязь.

H₀>H₁>H₂>…>H_n

Для русского текста H₀ = log₂32 = 5 бит; H₁ = 4,35 бит; Н₂ = 3,52 бит;

H₃ = 3,01бит, H₄ = бит.

Порой сообщения имеют некоторую избыточность

Пример – в телеграммах нет союзов;

– можно текст сократить в 2 раза и восстановить его.

Наличие избыточности увеличивает помехоустойчивость, но излишне загружает канал связи. Для принятия решения о увеличении или уменьшении избыточности надо измерять ее количественно.

т.к. Hn < H0, то

можно утверждать, что сообщения, у которых энтропия символов меньше max явл. избыточными.

Коэффициент избыточности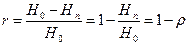

Коэффициент сжатия

Пример 4.3

Производительность источника отражает его динамические св-ва à кол-во инф., выдаваемое источником в ед. времени

Обозначим: τ_а – длительность символа

H’(A) – производительность источника

Производительность источника, если символы посылаются равномерно:

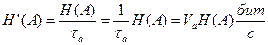(4.6)

В общем случае при определении производительности источников следует учитывать как скорость выработки символов, так и скорость посылки в канал сообщений, составленных из этих символов.

1.2. Энтропия источников непрерывных сообщений.

В отличие от дискретных сообщений, образованных счетным множеством элементов (символов a_i), символы алфавита непрерывных сообщений пронумеровать нельзя. Вер-ть каждого отдельного значения непрерыв. сообщ. ≠ 0, а распределение вер-ти характеризуются плотностью W(a).

Рассматривая энтропию непрерывных сообщений как мат-ожид. непрерывной С.В. и по аналогии с (4.3).

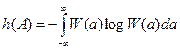(4.7)

Дифференциальная энтропия не имеет абсолютного хар-ра, зависит от масштаба и à не может служить мерой неопределенности источ. сообщ., даже способна принимать отрицательные значения.

играет важную роль при рассмотрении инф. хар-к с-м передачи, т.к. здесь имеют место разность энтропий.

а) При заданной средней мощности (дисперсии)максимальной энтропией обладают сообщения с нармальным з-ном распределения; б) Если задана пиковая мощность, то max энтропией обладают сообщения с равновероятным з-ном распред.

а) σ₂ = const

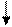var-з-ны распределения

нормальный з-н распределения

б) пиковая мощность = const var-з-ны распределения.

Равновероятный з-н распределения

Вопрос 2.

Информационное описание каналов связи.

Практически не существует с.м передачи без помех à Нет однозначности между символами и количеством инф. на вх. и вых. канала связи.

Обозначим

b₁, b₂, …, b_i, …, b_mk – символы на вх. канала; p(b_i) (априорные вероятности – до опасности).

b₁*, b₂*, …, b_j*, …, b_mk* – символы на вх. канала; p(b_j*)

В общем случае m_k ≠ m’_k. Например m_k = m_k+1 (добавляется символ «стирание»).

Нет однозначности à символ b_i с различной вер-тью может перейти в любой символ b_j* и наоборот, принятый символ b_j* может появиться в результате отправления любого из символов b_i, .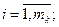

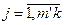p(b1/bj*) – апостериорная (после опыта) вер-ть передачи bi, если уже принят bj*. В принциме можно вычислить инф. потери для каждого конкретного символа, но больше интересуются обобщенной характеристикой – среднее кол-во инф. приходящейся на 1 символ.

Случай 1. Описание со стороны приемника.

b_mk p(b_mk/b_j*)

p(b_i/b_j*)

b_i

p(b₁/b_j*)

Рис. Неопределенность в дискретном канале с поме­хами (описание со стороны приемника)

b₁

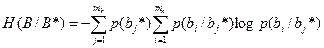à

Энтропия характеризует ср. кол-во инф. при условии, что уже стали известны принимаемые символы.

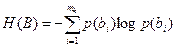
Ср. кол-во инф. посылаемое в канал с каждым символом:

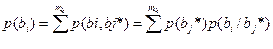
J(B,B*)=H(B) – H(B/B*)

прием передача потеря

Взаимная инф. между мн-вами В и В*, ср. кол-во инф., которое может принести получателю один символ в канале с помехами; ср. кол-во инф. содержащейся в символе мн-ва В* относительно символа мн-во В

Н(В) – ср. на символ кол-во инф. посланной в канал.

J(B,B*) – ср. на символ кол-во инф. принятой.

H(B/B*) – ср. на символ кол-во инф. потерянной в канале

(надежность канала)

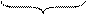
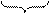0 ≤ H(B/B*) ≤ H(B)

Сильные помехи или обрыв связи – Знание b*(t) не уменьшает неопределенности b(t), т.е. b*(t) не содержат никакой инф. о b(t).

Помехи отсутствуют и b*(t) сожержит полную инф. о b(t), т.е. можно точно устано­ить последова­ель­ость передан­ых символов

Пример 4.4

Случай 2 Описание со стороны передатчика.

(b_m’k/b_i) b_m’k*

b_i p(b_j*/b_i) b_j*

p(b_j*/b_i)

b₁*

Рис. Неопределенность в дискретном канале с помехами (описание со стороны передатчика)

p(b_j*) – вер-ть того, что будет получен символ b_j*, если уже передан b_i.

p(b_j*) =

H(B*) = – 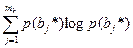- здесь часть инф. полезной (правильной) созданной b_i, а часть ложной, созданной помехами в канале связи.

H(B*/B) = -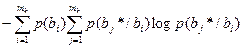

ср. инф., приходящаяся на 1 символ, содержащая b последовательных вых. символов b*(t) при известной последовательности вх. символов b(t) à инфопомех à энтропия шума

J(B,B*) = H(B*) – H(B*/B) (4.9)

правильная шум

(плезная)

Пример 4.5.

Формулы (4.8) и (4.9) наглядно иллюстрируются рис.

передача Н(В) J(B, B*) (прием) H(B*) привильная (полезная)

H(B,B*) H(B*/B)

(потеря) (энтропия шума)

Каждый из наборов p(b_i), p(b_j*/b_i) и p(b_j*), p(b_i/b_j*) явл. информационно полным, т.к. с помощью любого из них путем алгебраического преобразования можно получить все др. инф. хар-ки канала.

Для непрерывного канала

Если канал имеет ограниченную полосу пропускания F, то с-лы B(t) на его вх. и с-лы B*(t) на его вых. в соответствии с теоремой Котельникова определяются своими отсчетами, взятыми через интервал Δt = 1/2F. Такая замена позволяет описать ср. кол-во инф., содержащейся в одном вых. отчете, относительно одного вх. отсчета, соотношениями аналогичными (4.8), (4.9).

J(B,B*) = h(B) – h(B/B*) = h(B*) – h(B*/B).

Тема 4. Информационные основы передачи сообщений по каналам связи.

Лек. 7. Согласование источников сообщений с каналами связи.

1. Скорость передачи информации и пропускания способность каналов связи.

1.1 Скорость передачи информации и пропускания способность каналов связи дискретного канала.

1.2 Скорость передачи информации и пропускания способность каналов связи непрерывного канала.

2. Теорема Шеннона для дискретного канала без помех.

2.1 Дискретный канал без помех.

2.2 Теорема Шеннона.

2.3 Статистическое кодирование.

3. Возможности помехоустойчивого кодирования.

Вопрос 1

1.1

τ_k – длительность символов b_i и b_j*.

В канале с помехами в ед. времени в среднем передается кол-во инф.

J’(B, B*) = J(B, B*) / τ_k = V_k[H(B) – H(B/B*) = V_k[H(B*) – H(B*/B)] (4.10)

В (4.10) – скорость передачи инф. по каналу зависит как от источника дискретного сигнала (Н(В)), так и от св-в канала.

А найти надо способность самого канала передавать инф.

Пропускания способность канала – max возможная скорость передачи инф. при заданных св-вах канала.

С = max J’(B, B*) = V_k max J(B, B*) (4.11)

p(b_i) p(b_i)

Максимизация выбором p(b_i) при заданных v_k и m_k.

Пример 4.6.

p(b₁*/b₁) = 1 – P_ош

– p(b₂*/b₁) = P_ош

– p(b₁*/b₂) = P_ош

p(b₂*/b₂) = 1 – P_ош

Рис. Двоичный симметричный канал связи.

Если в канале связи помехи одинаково влияют на передаваемые символы, то канал симметричный (все вер-ти ложных приемов одинаковы, все вер-ти привильных приемов одинаковы.

C = V_k max[H(B*) – H(B*/B)]

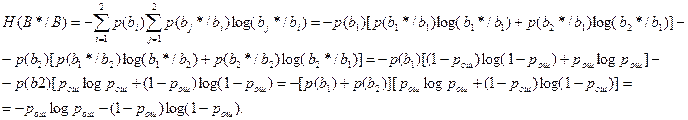
H(B*/B) от p(b_i) – не зависит.

H(B*)_max = 1 при b₁* и b₂* независимых и равновероятных à

С = V_k[1+р_ошlogр_ош + (1-р_ош)log(1-р_ош)]

1. р_ош = 0, Сmax = v_k, р_ош – вероятность ошибочного приема символа.

2. р_ош = 0,5. Обрыв канала – полностью исчезает связь между пердаваемыми и принимаемыми символами.

3. р_ош = 1 – также как при р_ош = 0. Все принимаемые символы надо инвертировать.

1.2. Скорость передачи информации и пропускания способность непрерывного канала.

C = V_k max J(B, B*), V_k = 1/τ_k = 2F_k V_k – частота дискретизации.

W(b)

Рассмотрим аддитивную помеху (b* = b + n)

J(B, B*) = h(B*) – h(B*/B)

Апостериорное распределение вер-тей W (b*/b) при любом фиксированном с-ле будет определяться з-ном распределения помехи W(n) и соответственно h(B*/B) равна энтропии

W(n) à W(b*/b); h(b*/B) = h(N)

C = V_k max[h(B*) – h(N)

При заданной мощности (дисперсии) помехи P_п = Б_п2 ее дифференциальная энтропия max и равна 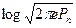при нормальном распределении à С при этом min.

Значит Гауссова помеха наиболее опасна для передаваемой инф.

Зная хар-ки помехи N и смеси с-ла с помехой B*, определим требования к с-лу В при выполнении которых обеспечивается max h(B*)

max h(B*) = log 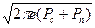при

W(b)

1) т.к. спектральные плотности помехи и смеси с-ла и помехи равномерны à спектральная плотность с-ла также равномерна.

2) т.к. помеха и смесь с-ла и помехи имеют нормальное распределение à плотность вероятности с-ла также имеет нормальный з-н распределения.

С = V_k max J(B, B*) = 2F_k(log – ).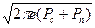

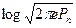С = F_k log(1+P_c/P_n) (4.12)

формула Шеннона указывает теоретический предел скорости передачи инф. по каналу связи с помехами.

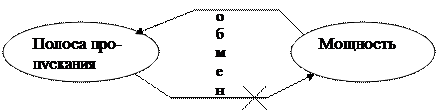да

С зависит от F линейно, а от P_c/P_п – по логарифмическому з-ну à обмен мощ­ности на полосу пропускания эффективен, обратный обмен нецелесообразен.

Рассмотрим С(F_k) = F_k log(1+p_c/F_kN₀)

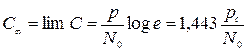(4.13)

С увеличением пропускания способность быстро возрастает, и затем ассимптотически стремится к С_∞.

Рис. Зависимость пропускной способности гаусовского канала от его полосы пропускания

J_k = T · C = F_k · T · log(1 + p_c/p_п) – количество инф., которое может быть передано за время Т (произведение 3-х сомножителей).

При уменьшении значения одного сомножителя неизменность произведения обеспечивается увеличением знач. др. сомножителей. Но С не может превысить С_∞ даже при F_kà∞, при этом

ТС < ТС_∞ = 1,443(p_cT/N₀) à для передачи 1 бита инф. необходимо иметь h₀=p_cT/N₀ > 0,693

Примечание. Если помехи имеют неравномерный спектр или же з-н их распределения отличается от нормального, то пропускная способность канала может превысить значение, вычисление по формуле (4.12).

Вопрос 2.

Теорема Шеннона для дискретного канала без помех.

2.1. Дискретный канал без помех.

Один из основных вопросов теории передачи информации à Возможно ли передать инф. без потерь со скоростью, равной пропускной способности канала? Если ДА, то КАК?

Рассмотрим идеализированный случай, когда действиями помех можно пренебречь. Для повышения эффективности с.м. связи широко исп. кодирование сообщений.

Кодирование:

алфавит сообщений А = {a_i}, i = 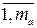, ­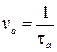 – скорость выработки сообщ.

алфавит кодовых символов 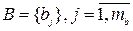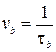– скорость передачи символов.

Получаем:

v_k = v_{k max} à J’max при H(B)_max, что возможно равновероятности кодовых символов, т.е. H(B)_max = log m_k.

C = J’(B, B*)_max = v_kH(B)_max = v_k log m_k

при двоичном кодировании = 1

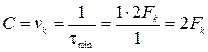(4.14)

Большинство реальных источников сообщ. обладает избыточностью в следствие:

Энтропия этих источников меньше max, т.е. каждый символ в среднем несет меньше кол-во инф., чем мог бы нести.

а) отличие з-на распределения вер-тей появления символов от равномерного.

б) наличием связей (зависимостей) между символами.

Пример: русский алфавит 32 буквы, при двоичном коде, т.е. при m_k = 2, код будет 5-ти разрядным (5 символов 0 или 1). Если алфавит равновероятный, то каждая буква (код 5-ти разрядный) переносят 5 бит, а каждый символ 1 бит.

Реально каждый символ в среднем переносит 0,6 бит. à скорость передачи инф. меньше пропускной способности канала. Символ кода при одной и той же длительности τ_k мог бы доставлять в сек 1/ τ_k бит информации, а доставляет 0,6/τ_k бит.

Но можно использовать эффективные коды и обеспечить скорость передачи инф. близкую к пропускной способности канала.

2.2. Теорема Шеннона для дискретного канала без помех.

Если производительность источника сообщений H’(A) не превышает пропускную способность канала связи С

Н’(А) ≤ С, то

существует способ кодирования, позволяющий передавать по каналу все сообщения источника, причем средняя скорость передачи букв сообщения v_a может быть увеличена при любой статистике источника до значения сколь угодно близкого к С/Н(А), энтропия Н(А) = log m_a.

Энтропия источника сообщ. при равновероятн. H(A) = log m_a, c=v_kH(A) = v_klogm_a.

v_k = C/H(A)

Теорема очевидна, если символы источника независимы и равновероятны. А если нет?

2.3. Статистическое кодирование.

Пример А. Источник выдает 4 шт равновероят. буквы. Н₀ = 2 бит. Эф. код а₁ – 00; а₂ = 01; а₃ = 10; а₄ =11. Число символов кода, приходящихся на 1 букву равно энтропии à полное согласование и источника и канала.

Пример В. Источник выдает 4шт неравновероятные буквы p(a₁) = 0,5; p(a₂)=0,25; p(a₃) = p(a₄) = 0,125.

Энтропия источника H₁(A) = 1,75 бит. Применяя код из примера А, на каждую букву затратим 2 кодовых символа (2 бита). Но из теоремы следует, что можно более экономичное кодирование с затратой на каждую букву в среднем 1,75 дв. кодовых символов.

Разработано много методов эффективного кодирования среди которых статистическое кодирование.

Суть – неравномерные коды, более часто встречающиеся сообщ. источника отображаются более короткими кодовыми комбинациями.

Впервые предложены Шенноном и Фено.

Методика: символы алфавита источника выписываются в порядке убывания вер-тей. Затем они разделяются на 2 гр. так, чтобы ∑ ветвей в каждой из групп были бы по возможности одинаковыми. Первой гр. присваивается кодовый символ 0, второй 1. Каждая из полученных групп (если там более 1 сообщ.) в свою очередь разбивается снова на две подгруппы, вновь первой присваивается символ 0, второй 1 и т.д.

а1, а2, а3, а4 a1 à 0

0,5 0,25 0,125 0,125 a2 à10

a3 à 110

0 1 a₄ à 111

0,25 0,125 0,125

0 1

0,125 0,125

0 1

Ср. кол-во кодовых символов, приходящихся на 1 букву

,

т.е. равно энтропии источника.

Если вер-ти появл. символов источника не явл. целочислен. степенями двойки, то невозможно произвести разбиение на группы с равными ∑-ными вероят. Тогда рез-ты будут более худшими.

Для увеличения эффектив. кода в этом случае переходят от кодирования одиночных символов к кодированию сообщений, составленных из большего кол-ва символов (блочное или укрупненное кодирование). Чем больше символов в блоке, тем больше будет символов, которые не зависят от предыдущих блоков. Происходит декореляция кодов.

Кодирование с целью экономного представления инф. в чистом виде в реальных каналах – нецелесообразно, т.к. процесс декодирования становится сесьма чувствительным к воздействию помех.

Вопрос 3.

Возможности помехоустойчивого кодирования.

Если влиянием помех в канале связи пренебречь нельзя, то помимо вопроса о повышении эффективности, возникает еще более важный вопрос – повышение верности передачи. Чем интенсивнее помеха, тем меньше пропускная способность отдав дань помехам в виде уменьшения пропускной способности.

Вопрос. нельзя ли организовать передачу сообщений, чтобы и вероятность ошибочного декодирования были бы сколь угодно малой и скорость передачи информации по каналу приближалась к пропускной способности ее создания источником?

Если ДА, то КАК?

Ответ. Основная теорема Шеннона для дискретного канала помехами.

Суть теоремы:

Если производительность источника не превышает пропускную способность канала связи H’(A) ≤ C, то существует способ кодирования позволяющий передавать по каналу все сообщения источника со сколь угодно малой вероятностью ошибки, при этом скорость передачи инф. может быть сколь угодно близкой к скорости ее создания источником.

Теорема доказывает универсальный хар-р условия H’(A) ≤ C для передачи инф. без потерь.

Кодирование, повышающее верность передачи по каналу с помехами наз. помехоустойчивым или корректирующим.

Помехоустойчивость может быть достигнута сравнительно просто за счет многократного повторения, но скорость передачи инф. при этом снижается.

Для обеспечения достоверной передачи инф. достаточно ввести во вх. сообщ. избыточность, несколько превышающую потерю инф. в канале из-за действия помех, характеризуемую ненадежностью канала H(B/B*). Удлинение же кодируемых последовательностей при исп. таких кодов вызывает не уменьшение пропускной способности, а лишь увеличение задержки в приеме инф.

Теорема Шеннона не указывает конкретного способа кодирования, а лишь доказывает его принципиальное существование, а также то, что С – это предельное значение скорости безошибочной передачи инф. по каналу.

Общий подход к кодированию à «кодирование длинных сообщений, а не отдельных символов». При этом достоверность связи тем выше, чем более длинными блоками осуществляется кодирование и чем менее эффективно исп. пропускная способность.

В свою очередь это:

а) требует большой емкости памяти (запомнить длинные блоки);

б) приводит к большой задержки передачи;

в) обуславливает сложность кодирующих и декодирующих уст-в.

Поэтому чаще всего увеличение верности передачи добиваются за счет менее полного использования пропускной способности канала путем введения спец. избыточности в кодовые комбинации.

Для непрерывного канала его пропускная способность явл. также и верхней границей скорости достоверной передачи инф. При этом достоверная передача инф. со скоростью, приближаюейся к пропускной способности, возможна лишь при кодировании с-лов очень большой длительности (также как в дискретных каналах).

Тема 5. Прием сигналов в системах передачи дискретных сообщений.

Лекция 8. Оптимальный прием дискретных сигналов по критерию Идеального Наблюдателя.

1. Ф-ция правдоподобия в критерии идеального наблюдателя.

2. Алгоритм оптимального приема полностью известных сигналов.

3. Структурная схема оптимального приемника.

Оптимизация приемной части с-мы передачи явл. основой построения с-м, которые обеспечивали max достоверность, при наличии помех в канале. Частными задачами при этом явл.:

1) выбор структуры приемной части с-мы;

2) оценка верности передачи при различных условиях;

3) разработка путей совершенствования реальных с-м.

Вопрос 1

Впервые задача оптимального приема для канала с постоянными параметрами, при наличии аддитивной помехи типа нормального белого шума была решена сов. ученым В.А. Котельниковым в 1946г. Этот классический подход лежит в основе решения других более сложных задач оптимального приема дискретных с-лов.

x(t) = S_i(t) + n(t),

где x(t) – эл. колебание на вх. приемника (аддитивная смесь);

S_i(t) – полезный с-л в ме приема, т.е. с-л U_i(t) прошедший канал связь;

n(t) – помехи.

После ряда преобразований – фильтрации, усиления, переноса по частоте и т.п., которые в данном рассмотрении не существенны, смесь с-ла с шумом x(t) поступает на вх. демодулятора.

Именно демодулятор «принимает решение» - какой из возможных с-лов U_i(t) содержится в принятом колебании (à какой кодовый символ b_i был передан).

При наличии помех в канале приемник (демодулятор) не может точно воспроизвести передаваемое сообщ. Он лишь «угадывает» с той или иной степенью точности. Вполне естественным требованием к приемнику явл. проводить «угадывание» наилучшим образом. Тогда приемник будет оптимальным.

Понятие «наилучшим образом» требует уточнения и формализации. Среди прочих критериев оптимальности широко исп. критерий Котельникова – критерий идеального наблюдателя.

Суть критерия – оценивается и min-ется полная вероятность ошибочного приема символа.

Проведем формализацию критерия.

Обозначим:

p(b_i/x) – апостериорная (после опытная) вер-ть передачи символа b_i; вер-ть того, что в рез-те анализа колебания x(t) демодулятор принимает решение, что передан символ b_i.

Критерий Котельникова обеспечивается исп. правила max апостериорной вер-ти.

p(b_i/x) > p(b_j/x), i≠j.

Определить непосредственно условные вер-ти p(b_i/x) в приемнике невозможно, но их можно расчитать по фор. Байеса – формула обратной вер-ти (по вер-ти следствия находят вер-ть причины.

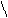Априорная вер-ть передачи символа b_i

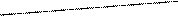
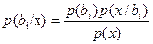условная и безусловная вер-ти появления колебания х на входе приемника

При аддитивной флуктуационной помехе колебания х явл. непрерывным à вместо p(x/b_i) и p(x) необходимо пользоваться плотностями распределения вер-тей W(x/b_i), W(x).

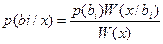
Регистрируется символ b_i, если

p(b_i)W(x/b_i) > p(b_j)W(x/b_j)

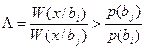
где W – ф-ция правдоподобия;

Λ – отношение правдоподобия.

Более правдоподобна та гипотеза, у которой большая плотность вер-ти получения данной реализации.

Правило максимума ф-ции правдоподобия 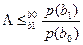. Правило решения оптимального приемника двоичных с-лов по критерию идеального наблюдателя.

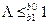- для случая равновероятной передачи b₀ и b₁.

Критерий идеального наблюдателя предполагает, что все ошибки одинаково нежелательны. На практике это не всегда так. «Значимость» различных ошибок, т.е. степень нежелательности их последствий можно учесть введением весовых коэффициентов, приписываемых каждому ошибочному решению. В таком случае критерий наз. критерием минимального среднего риска (min средних потерь).

Вопрос 2.Алгоритм оптимального приема полностью известных с-лов.

Чем полнее сведения о сообщениях, полезных с-лах и помехах, тем правильнее будет решение приемника. Наивысшая достоверность будет при полном знании априорных данных о сообщениях и помехах и при с-лах, известных точно. При этом помехоустойчивоть приема – max ­à потенциальная.

Прием ограничения (допущения) и обозначения.

b_i – передаваемый символ;

Ui(t) – передаваемый с-л;

x(t) = S_i(t) + n(t) – колебание на вх. приемника.

S_i(t) = KU_i(t – τ) – известны полностью (копии в памяти приемника).

Помеха – белый нормальный шум, N₀ – его спектральная плотность, моменты прихода с-лов известны.

Неизвестно: - конкретная реализация помехи;

- номер (i) действительно переданного с-ла (символа).

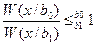, определим W(x/b_i)

Заменим белый шум с F à ∞ квазибелым, ограниченный полосой ч-т Δf. Тогда вместо n(t) можно взять дискретную выборку n(t₁), n(t₂) … n(t_k) …n(t_m)

Δt = 1/2 Δf

Одномерная плотность вер-ти.

W₁(n_k) = ,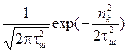

т.к. отчеты независимы, то многомерная плотность шума

W_m = W₁(n₁)·W₁(n₂) ·…· W₁(n_k) ·…· W₁(n_m).

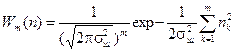(5.1)

где σ_ш² = N₀ · Δf – дисперсия (мощность) квазибелого шума.

x(t) = S_i(t) + n(t) ; n(t) = x(t) = S_i(t)

W(x/b_i) = W(x₁, x₂, …, x_m/b_i)

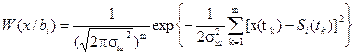
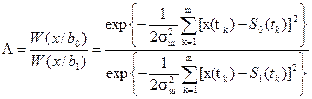
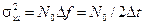
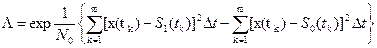(5.2)

Вернемся от квазибелого шума (в полосе Δf) к белому шуму.

Δf увеличивается, при этом m à ∞, Δt à 0, ∑ обратится в .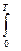

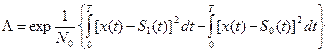
Алгоритм решения:

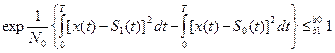(5.3)

Вопрос 3.

Структурная схема оптимального приемника.

Упростим (5.3) прологарифмировав по основанию с лев. и прав. части нер-ва.

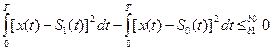(5.4)

Раскроем скобки:

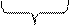
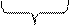
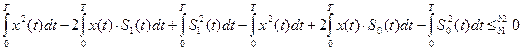
E₁­ E₀

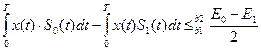(5.5)

Структурная сх. оптимального корреляционного приемника двоичных точно известных с-лов.

Если с-лы имеют одинаковую энергию, Е₀ = Е₁, то алгоритм (5.5) упрощается

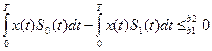(5.6)

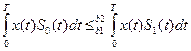(5.7)

Условие оптимального приема: если с-лы, используемые в с-ме связи, имеют одинаковую энергию, то оптимальный приемник воспроизводит сообщение, соответствующее тому переданному с-лу, взаимная корреляция которого с принятым колебанием максимальна

Преимущество: не требует знания «масштаба» приходящих с-лов (коэф. передачи канала). Это широко исп. на практике à с-лы с равной энергией (с-лы с активной паузой).

Недостаток: с-лы подаваемые на перемножители опорные и приходящие должны совпадать с точностью до фазы. Для этого исп. спец. уст-ва синхронизации. А такой оптим. приемник относится к типу когерентных. Кроме «тестирования» вх. с-лов перемножителя уст-во синхронизации управляет УСВ, взятие отсчетов, их сравнение и принятие решения производится в момент окончания с-ла. После всего этого необходимо произвести сброс напряжения с интегратора, тем самым подготовив его к обработке след. посылки.

Из-за использования в корреляторах активных цепей- генераторов их часто наз. активными фильтрами.

Возможен и др. путь реализации оптимального приемника – с помощью соответствующего пассивного линейного фильтра с постоянными параметрами.

Тема 5. Прием сигналов в с-мах передачи дискретных сообщений.

Лек. 9. Оптимальный приемник на базе согласованных фильтров.

1. Согласованный фильтр. Определения и хар-ки.

1.1. Требование к импульсной переходной хар-ке фильтра.

1.2. Требование к амплитудно-частотной и фазочастотной хар-кам фильтра.

1.3. Структурная схема оптимального приемника на согласованных фильтрах.

2. Методы синтеза согласованных фильтров.

2.1. Временной метод синтеза согласованных фильтров.

2.2. Спектральный метод синтеза согласованных фильтров.

Вопрос 1

1.1. Требование к импульсной переходной хар-ке фильтра.

Если определенным образом отобразить параметры с-ла в хар-ках фильтра, то им можно осуществлять оптимальный прием с-ла.

Одной из основных хар-к любого линейного фильтра является импульсная переходная хар-ка g(t) à физический отклик фильтра на единичный импульс. Описывает св-ва фильтра во временной области.

Идеальный единичный имп. (обобщенная дельта-ф-ция Дирака).