Профилактика машин и оптимизация межремонтных циклов

Рассмотрим четыре основные модели профилактики машин:

- с аварийными ремонтами;

- с плановыми ремонтами при внеплановых аварийных ремонтах без переноса сроков очередного технического обслуживания (ППР);

- с плановыми ремонтами при внеплановых аварийных ремонтах с переносом сроков очередного планово-предупредитель­ного ремонта;

- с плановыми ремонтами.

Аварийные ремонты имеют большое распространение. Предполагается, что отказ обнаруживается мгновенно в момент возникновения. В течение всего времени аварийного ремонта машина простаивает. По окончании ремонта весь процесс функционирования машины и ее обслуживания повторяется.

Очевидно, что при описанной модели профилактики может быть вычислен критерий K, однако нахождение его минимума бессмысленно.

Обозначим: t₃ – средняя продолжительность аварийного ремонта; b₃ – средние затраты на проведение аварийного ремонта (ремонта вследствие отказа); e₁ – средний ущерб в единицу времени простоя или средний ущерб от невыполнения устройством единицы работы; e₂ – средний ущерб от отказа устройства.

Здесь и далее будем считать, что эффект от эксплуатации машины пропорционален времени ее работы (наработке).

Тогда

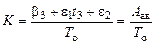, (5.27)

где А_ав – средние затраты, связанные с аварийным ремонтом;

Т_o – средняя наработка до отказа,

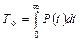. (5.28)

Плановые ремонты при внеплановых аварийных ремонтах. Такая система широко применяется для обслуживания горных и транспортных машин. Предполагаем, что возможно проведение плановых предупредительных ремонтов и аварийных ремонтов, причем отказ обнаруживается мгновенно. Восстановительные работы производятся в следующей очередности. Если машина не отказала к назначенному моменту, то производится плановый ремонт, если отказ системы произошел ранее, то в момент отказа начинается аварийный ремонт. После аварийного ремонта время очередного планового ремонта не изменяется. Предполагаем, что во время проведения плановых и аварийных ремонтов машина неработоспособна.

Обозначим:

t₁ – средняя продолжительность планового ремонта;

b₁ – средние затраты на проведение планового ремонта;

W(Т₁) – ведущая функция потока отказов – математическое ожидание числа отказов за время Т₁ – искомое время периодичности плановых ремонтов (без времени, затрачиваемого на аварийный ремонт t₃W(Т₁)).

Средние затраты, связанные с проведением одного планового ремонта за время Т₁, равны А_пл = b₁ + e₁ t₁. Затраты, связанные с проведением W(Т₁) аварийных ремонтов, будут равны А_авW(Т₁). Суммарные затраты за период Т₁ составят S_А = А_авW(Т₁) + А_пл.

Критерий оптимизации

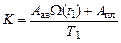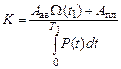или . (5.29)

Плановые ремонты при внеплановых аварийных ремонтах с перенесением времени проведения очередного планового ремонта. После проведения аварийного ремонта очередной плановый ремонт переносится таким образом, чтобы время между моментом окончания последнего аварийного ремонта и очередным плановым ремонтом было равно Т₁. Такая модель профилактики целесообразна для крупных, дорогостоящих узлов, имеющих длительный срок службы (приводы ленточных конвейеров, составные части комбайнов, электродвигателей электровозов и т.п.). Если Р(Т₁) – вероятность безотказной работы в течение времени Т₁, то средние затраты на проведение планового ремонта на периоде регенерации равны А_плР(Т₁).

Вероятность отказа в течение времени Т₁ равна 1 – Р(Т₁). Средние затраты на аварийные ремонты А_ав[1 – Р(Т₁)]. Среднее время наработки на периоде регенерации Т₁ равно .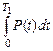

Критерий оптимизации

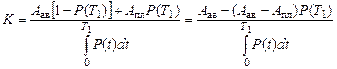. (5.30)

Плановые ремонты. В практике горной промышленности возможно применение только плановых ремонтов, назначенных по календарному времени (пример – шахтные электровозы). В этом случае отказ может быть обнаружен только при проведении планового ремонта. С момента отказа до окончания очередного планового ремонта машина не сможет выполнять свои функции.

Если Р(Т₁) – вероятность безотказной работы в течение времени Т₁ (искомое время периодичности плановых ремонтов), то средние затраты, связанные с проведением планового ремонта на периоде регенерации Т₁, равны А_плР(Т₁), средние затраты, связанные с проведением аварийного ремонта, равны А_ав[1 – Р(Т₁)], средний ущерб от простоя из-за необнаружения отказа на интервале времени от момента отказа до проведения очередной замены равен

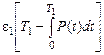, (5.31)

поскольку средняя наработка машины на периоде регенерации Т₁ равна .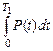

Для данной стратегии обслуживания критерий оптимизации

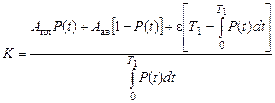. (5.32)

После выбора оптимального срока замены различных деталей они могут быть сгруппированы по срокам их замены и, в зависимости от сложности ремонта, могут быть назначены ТО, текущий или капитальный ремонт. Желательно, чтобы структура ремонтного цикла была кратной, т.е. при каждом последующем виде ремонта производилась замена деталей и сборочных единиц всех предыдущих групп.

Узлы и детали горных машин имеют разброс наработок до отказа, поэтому необходимо правильно выбирать интервалы профилактической замены для различных групп деталей.

Профилактическая замена деталей через период, равный минимальной наработке до отказа, является экономически неоправданной, так как многие детали при замене будут иметь еще достаточный ресурс и, кроме того, потребуются затраты на преждевременную замену, при этом уменьшится коэффициент технического использования машины. При максимальных сроках замены увеличится опасность аварийного отказа, связанного с возможными тяжелыми последствиями. Необходимо выбирать оптимальные интервалы плановых замен деталей, т.е. планировать сроки ремонтного обслуживания.

Оптимальные интервалы между плановыми заменами деталей определяются на основании различных критериев:

- максимального коэффициента технического использования;

- минимальных затрат на обслуживание и др.

В горной промышленности наиболее распространенными являются экономические критерии.

К оптимизации периодичности плановых замен деталей следует подходить с учетом не только затрат при эксплуатации, но и эффекта от использования машины.

Рациональной будет такая организация замен, при которой от каждой единицы затрат будет получен максимальный эффект.

В общем виде критерий оптимизации

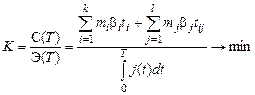, (5.33)

где С(Т) и Э(Т) – соответственно суммарные затраты и суммарный эффект за время эксплуатации Т;

j(t) – математическое ожидание мгновенного значения эффекта от использования машины;

k – количество видов работ по обслуживанию;

m_i – количество работ по обслуживанию i-го вида;

b_i – средние затраты за единицу времени при проведении i-го вида работы по обслуживанию;

t_i – средняя продолжительность проведения i-го вида работы по обслуживанию;

l – количество причин простоев;

m_j – количество простоев по j-й причине;

b_j – средний ущерб за единицу времени простоя по j-й причине или ущерб от невыполнения конкретного задания;

t_j – средняя продолжительность простоя по j-й причине.

Можно показать, что при достижении минимума критерием оптимизации K одновременно получается минимум суммарных затрат, минимум удельных затрат, связанных с эксплуатацией устройства, максимум коэффициента технического использования и максимум коэффициента готовности.

Определение оптимальных сроков службы элементов машин может быть выполнено только для принятой модели профилактики. После проведения любой из возможных замен считается, что показатели надежности элемента полностью восстанавливаются, и назначается следующая плановая замена через период Т.

Задача состоит в отыскании такого значения этого периода (часы, сутки), при котором значение критерия оптимизации будет минимальным.

Рассмотрим методику на примере модели профилактики с плановыми и аварийными ремонтами.

Значение критерия оптимизации для этой модели:

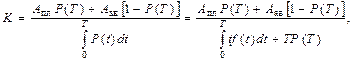(5.34)

где 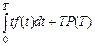– математическое ожидание наработки при условии замены элемента, если его наработка достигнет величины Т.

Разделив левую и правую части уравнения на А_ав, получим

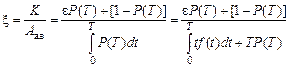, (5.35)

где e = А_пл/А_ав – коэффициент стоимости.

Приняв 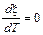, получим

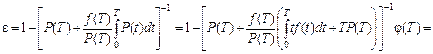(5.36)

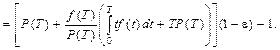
Локализация корней может быть произведена из следующих соображений:

1. При нормальном распределении Р(Т) уравнение имеет только один корень, который с вероятностью 0,997 находится в интервале [t_ср – 3s; t_ср + 3s]. Так как этот корень может быть только положительным, то следует принимать интервал [0; t_ср + 3s]. Здесь t_ср – математическое ожидание наработки; s – среднеквадратичное отклонение.

2. При распределении Вейбулла с параметром b > 1 уравнение имеет только один корень, который с вероятностью 0,982 находится в интервале [0; 4а].

3. При g-распределении уравнение имеет только один корень при условии, что e £ 1 – 1/m. Если e > 1 – 1/m, то уравнение не имеет корней. При отыскании корня следует рассматривать интервал .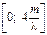

4. При логарифмически-нормальном распределении кривая x = f(Т) (рис. 5.3, а) имеет минимум и максимум. Поэтому уравнение при фиксированном e имеет два корня или вообще корней не имеет. Нижней границей интервала локализации корня является 0, верхнюю – нужно находить путем последовательного расширения интервала.

Метод половинного деления:

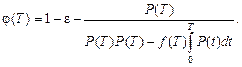(5.37)

a) б)

Рис. 5.3. Логарифмически-нормальное распределение:

а - экстремумы функции; б - поиск корня уравнения

Два корня уравнения – положительный и отрицательный. Предположим, известен интервал [a; b], внутри которого находится корень уравнения (рис.5.3, б). Вычислим значения j(а) и j(b). Если j(а)j(b)< 0, это значит, что функция j пересекает ось Т и искомый корень имеется в исследуемом интервале. Если j(а)j(с)> 0, значит корень уравнения находится в интервале [с; b]; если j(а)j(с) < 0, то корень находится в интервале [a; с].

Интервал локализации корня может быть сужен до любых пределов. Задается точность расчета [b – а] £ d. В этом интервале может быть принято любое значение Т.