Число наблюдений для основных законов распределения
| Закон распределения | Исходные параметры | Необходимое число наблюдений | ||
| b | d | Коэффициент вариации V | ||
| Экспоненциальный | 0,8 0,8 0,9 0,9 | 0,2 0,1 0,2 0,1 | ||
| Нормальный | 0,9 0,8 0,9 0,8 | 0,1 0,1 0,2 0,1 | 0,2 0,3 0,3 0,2 | |
| Логарифмически-нормальный | 0,9 | 0,2 0,2 0,1 0,1 | 0,4 0,7 0,4 0,7 | |
| Вейбулла | 0,8 | 0,2 0,2 | 0,6 0,8 | |
| 0,8 | 0,1 0,1 | 0,5 0,8 | ||
| 0,9 | 0,2 0,1 | 0,6 0,8 |
Для невосстанавливаемых или неремонтируемых объектов
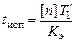 , (5.6)
, (5.6)
где [n] – минимально необходимое число объектов;
T1 – предполагаемая величина средней наработки до отказа.
Разовая продолжительность хронометражных наблюдений равна обычно продолжительности рабочей смены. Требуемое число смен
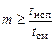 . (5.7)
. (5.7)
Длительность разовых хронометражных наблюдений должна быть больше 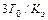 , а число смен непрерывных хронометражных наблюдений
, а число смен непрерывных хронометражных наблюдений
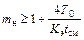 . (5.8)
. (5.8)
Для получения достоверных данных о законе распределения должно соблюдаться условие 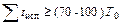 .
.
Определение показателей надежности связано с решением двух главных задач математической статистики – оценки неизвестных параметров выборки и проверки статистических гипотез.
Аналогией математического ожидания mх случайной величины х является его статистическая оценка (среднее арифметическое значение):
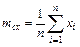 . (5.9)
. (5.9)
Число интервалов
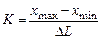 , (5.10)
, (5.10)
где DL – длина интервала.
Число интервалов K должно быть не меньше 5-6 и не более 10-12.
Число значений ni случайной величины х в каждом интервале должно быть не меньше 5.
Пример. Принимаем tmin = 0 при n = 300, tmax = 400 мин, тогда
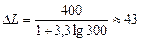 мин.
мин.
Обработка статистической информации.В связи с ограниченностью выборки из генеральной совокупности (из всего множества однотипных машин) статистическая функция распределения всегда содержит элементы случайности. Поэтому значения параметров для генеральной совокупности можно получить лишь с некоторой вероятностью. Такие значения параметров называются оценками. Оценкой функции распределения генеральной совокупности является статистическая функция распределения.
Закон распределения, если он неизвестен, определяется следующим образом.
Весь диапазон полученных значений случайной величины 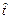 разбивается на интервалы. Для удобства расчетов интервалы целесообразно принимать равными.
разбивается на интервалы. Для удобства расчетов интервалы целесообразно принимать равными.
Примерная величина интервала
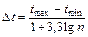 , (5.11)
, (5.11)
где n – количество полученных значений случайной величины 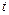 .
.
В каждом интервале количество значений случайной величины должно быть не менее 5-10. При меньшем количестве интервалы принимают разной длины. Для каждого интервала подсчитываются:
- число значений случайной величины, попавших в этот интервал ni;
- отношение ni/n (частота события).
Сумма 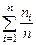 должна быть равна единице. Это – показатель правильности расчетов.
должна быть равна единице. Это – показатель правильности расчетов.
Доверительным называется интервал, который с вероятностью b покрывает оцениваемое значение параметра распределения. Величина вероятности b называется доверительной вероятностью. Если в результате опытов получена статистическая оценка параметра 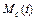 и установлено, что разница между параметром
и установлено, что разница между параметром 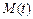 и его оценкой не превосходит некоторое значение e с вероятностью b, т.е.
и его оценкой не превосходит некоторое значение e с вероятностью b, т.е.
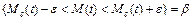 , (5.12)
, (5.12)
то интервал 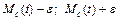 будет являться доверительным интервалом для оценки
будет являться доверительным интервалом для оценки 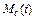 ; границы интервала называются доверительными границами. Коэффициент вариации
; границы интервала называются доверительными границами. Коэффициент вариации 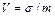 .
.
Если закон распределения до начала наблюдения неизвестен, то предполагается, что наработка на отказ и время восстановления распределяются по экспоненциальному закону, а ресурс и срок службы – по логарифмически-нормальному, т.е. в этом случае требуется выполнять максимальное число наблюдений.
Доверительная вероятность связана с предельной абсолютной ошибкой e условием
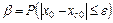 , (5.13)
, (5.13)
где 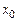 – генеральная средняя величина изучаемого признака;
– генеральная средняя величина изучаемого признака;
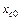 – оценка
– оценка 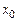 по результатам опыта.
по результатам опыта.
Относительная предельная ошибка 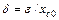 .
.
Затем на гистограмме строится теоретическая кривая распределения f(t), которая должна сохранить существенные особенности статистического распределения.
При подборе теоретической кривой f(t) между ней и статистическим распределением неизбежны некоторые расхождения.
Правильность выбора теоретической кривой устанавливается с помощью критерия согласия 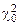 (критерий Пирсона):
(критерий Пирсона):
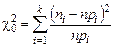 , (5.14)
, (5.14)
где k – количество интервалов статистического распределения; ni – количество значений случайной величины в i-м интервале; n – общее число значений случайной величины; рi – теоретическая вероятность попадания случайной величины в i-й интервал, равная приращению функции распределения в данном интервале.
Распределение 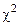 зависит от числа степеней свободы:
зависит от числа степеней свободы:
r = k – s – 1, (5.15)
где k – количество интервалов;
s – количество связей, для экспоненциального распределения s = 1, для нормального s = 2.
Для распределения 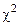 имеется табл.5.4, в которой приводятся корни уравнения
имеется табл.5.4, в которой приводятся корни уравнения
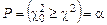 , (5.16)
, (5.16)
где a – уровень значимости (вероятность отвергнуть правильную гипотезу).
В практических расчетах принимают a = 0,05. В табл. 5.4 даны значения величины 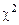 в зависимости от числа степеней свободы r и уровня значимости a.
в зависимости от числа степеней свободы r и уровня значимости a.
По a и r находят 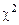 . Если
. Если 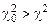 , гипотеза отвергается, так как мера расхождения
, гипотеза отвергается, так как мера расхождения 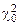 попала в критическую зону. Если
попала в критическую зону. Если 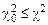 , – гипотеза принимается.
, – гипотеза принимается.
Определение параметров распределения. Параметры распределения определяются до и после выбора закона распределения на основе анализа гистограммы.
При любом законе распределения изучаемой величины оценка математического ожидания принимается равной среднему арифметическому:
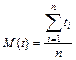 . (5.17)
. (5.17)
Оценка дисперсии
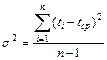 . (5.18)
. (5.18)
Среднеквадратическое отклонение
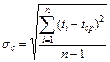 . (5.19)
. (5.19)
Коэффициент вариации
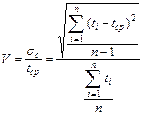 . (5.20)
. (5.20)
При нормальном законе распределения полученные оценки математического ожидания 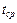 и среднеквадратичного отклонения s являются параметрами распределения.
и среднеквадратичного отклонения s являются параметрами распределения.
При логарифмически-нормальном распределении оценки параметров
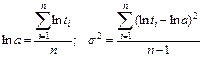 (5.21)
(5.21)
или оценки параметров могут быть получены через математическое ожидание и среднеквадратичное отклонение (через коэффициент вариации):
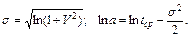 (5.22)
(5.22)
При экспоненциальном распределении математическое ожидание и дисперсия соответственно равны
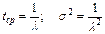 . (5.23)
. (5.23)
Следовательно, параметр распределения
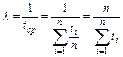 . (5.24)
. (5.24)
Для определения значений пi в анализируемом распределении строится гистограмма эмпирической плотности распределения случайной величины. По оси абсцисс откладываются интервалы Dt случайной величины и на каждом из этих интервалов строится прямоугольник с площадью, равной частоте появления случайной величины в данном интервале. Высоты прямоугольников пропорциональны частотам появления пi случайной величины в каждом интервале.
Длину интервалов рекомендуется определять по формуле
Dt 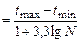 , (5.25)
, (5.25)
где tmax и tmin – соответственно максимальное и минимальное значения случайной величины в вариационном ряду.
Пример построения гистограммы и сглаживающей эмпирической кривой показан на рис. 5.2.

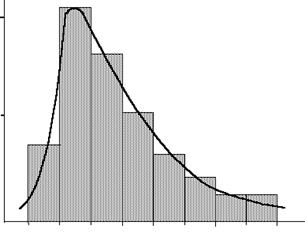
Рис. 5.2. Гистограмма и теоретическая функция распределения
Схема применения критерия c2 в оценке согласованности теоретического и статистического распределений сводится к следующему:
1) для каждого из исследуемых распределений определяют меру расхождения c2;
2) для каждого из распределений вычисляют число степеней свободы
r = k - s – 1, (5.26)
где s – количество независимых связей, равное числу определяемых параметров закона распределения;
3) по r и расчетным значениям c2, пользуясь приложением А, находят уровень значимости a критерия согласия для каждого исследуемого закона распределения, причем a должно быть не менее 0,01;
4) в качестве теоретической функции распределения принимается та, для которой уровень значимости получился наибольшим.
Дата добавления: 2020-05-20; просмотров: 819;











