Измерение скорости света

1. Скорость распространения света в пространстве – одна из важнейших проблем в физике. Её решение оказалось очень плодотворным для понимания физической картины мира. Скорость света в вакууме с – одна из фундаментальных физических постоянных. Огромная роль её в современной физике определяется тем, что она представляет собой предельную скорость распространения любых физических воздействий и инвариантна при переходе от одной системы отсчёта к другой. Никакие сигналы не могут быть переданы со скоростью большей с, а со скоростью с их можно передать лишь в вакууме.

Величина с связывает массу m и полную энергию Е материального тела, Е = mc². Через неё выражаются преобразования координат, скоростей и времени при переходе от одной системы отсчёта к другой. Она входит во многие другие соотношения физики.

При измерении скорости света в веществе стало глубже понимание сложной структуры явления скорости. Было установлено различие между скоростью распространения фазы электромагнитной волны (фазовая скорость) и скоростью распространения энергии (групповая скорость). Только в вакууме эти скорости совпадают. Во всех измерениях скорости света определяется групповая скорость.

2. Измерение скорости света методом Галилея. Впервые идею опытного определения скорости света высказал Галилей в 1638 г. в книге “Беседы и математические доказательства ...”. Два экспериментатора, вооружённые фонарями, становятся на известном расстоянии друг от друга. Когда один из них открывает фонарь, засекая момент времени, другой ждёт с закрытым фонарём. Он открывает его, как только увидит свет первого фонаря. Увидев свет второго фонаря, первый экспериментатор снова засекает время. По мысли Галилея, скорость света найдётся как отношение удвоенного расстояния между наблюдателями к промежутку времени между двумя засечками.

Попытки реализации этой идеи, предпринятые через два десятилетия во Флоренции, показали, что скорость света настолько велика, что измерить её таким путём невозможно. Время реакции человека много больше времени распространения света между наблюдателями в земных условиях. Но заслуга Галилея состоит в том, что он перенёс проблему скорости из формы абстрактного обсуждения (конечна или бесконечна) в форму практического измерения.

3. Астрономический метод Рёмера. В 1610 году с помощью изобретённой им зрительной трубы (труба Галилея, §9) Галилей открыл 4 самых крупных спутника Юпитера. Она назвал их (в порядке удаления от Юпитера) Ио, Европа, Ганимед, Каллисто. В связи с бурным развитием мореплавания появилась идея использовать периодичность восхода и захода этих спутников в качестве точного хронометра.

В 1672 г. астроном Джованни Кассини обнаружил нарушения в периодичности выхода из тени Юпитера его спутника Ио. Причём, с удалением Земли от Юпитера промежутки времени между восходами увеличивались, а с приближением - уменьшались.

В 1676 г., исследуя это явление, Олаф Рёмер высказал мысль, что скорость распространения света конечна. Схема рассуждений Рёмера такова. Когда Земля в своём движении вокруг Солнца удаляется от Юпитера, т.е. идёт от точки В к точке А (рис.213), то промежутки времени между моментами выхода Ио из тени Юпитера увеличиваются, поскольку свету нужно дополнительное время чтобы догнать убегающую Землю.

С приближением Земли ситуация меняется. Промежутки времени между восходами Ио уменьшаются, поскольку каждый последующий световой луч восходящего спутника проходит по сравнению с лучом предыдущего восхода меньшее расстояние.

Пусть Т – период обращения Ио вокруг Юпитера в системе отсчёта Юпитера, Т=42 часа 28 мин; Т_1i – промежутки времени между восходами Ио, измеренные с убегающей Земли; Т_2i – промежутки времени между восходами, измеренные с приближающейся Земли. Промежутки Т_1i и T_2i в течение года изменяются. Их значение зависит от того, в какой точке орбиты находится Земля. За полгода наблюдений с убегающей Земли (движение Земли от В к А) общая сумма промежутков между восходами составляет 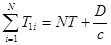, (26.1)

где N – число заходов за полгода, с – скорость света, D – диаметр орбиты Земли.

Для приближающейся Земли (движения от А к В) . (26.2)

Вычтя из 1-го уравнения второе, получаем: 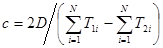. (26.3)

Для определения знаменателя совсем не обязательно измерять все промежутки времени между моментами восхода в течение года. Достаточно определить лишь разницу во времени между моментами восхода по прогнозу NT и реальным моментом восхода в самой дальней и самой ближней к Юпитеру точках орбиты Земли.

По измерениям Рёмера разница во времени å₁ - å₂ составила около 22 минут. К этому времени (1676 г.) уже утвердилась система мира по Копернику, были освоены законы Кеплера и был вычислен диаметр орбиты Земли D = 3·10¹¹ м. Поэтому Рёмер смог вычислить скорость света, с = 3·10¹¹½22·60 = 2,3·10⁸ м/с.

Из измерений Рёмера следовало, что скорость света имеет гигантское значение по сравнению со скоростью всех остальных процессов, наблюдавшихся на Земле.

4. Астрономический метод аберрации света Брадлея (от лат. аberratio – уклонение). В 1725 г. астроном Джеймс Брадлей предпринял попытку измерить годичный параллакс звёзд, то есть обусловленное вращением Земли кажущееся смещение близких к Земле звёзд на фоне более далёких.

В общем случае кривая параллактического смещения звезды должна выглядеть как уменьшен-ная проекция орбиты Земли на плоскость, перпен-дикулярную к направлению на Звезду (А на рис.214).

Если Звезда лежит в плоскости эклиптики (то есть в плоскости земной орбиты), то в течение года она смещается по прямой (В на рис.214).

В общем случае параллактическое движение звезды происходит по эллипсу, эксцентриситет которого (вытянутость) тем больше, чем ближе к плоскости земной орбиты находится звезда. Большая ось эллипса параллактического смещения параллельна плоскости эклиптики (С на рис.214).

Наблюдая γ – Дракона (примерно 50º к плоскости эклиптики), Брадлей обнаружил, что большая ось эллипса смещения звезды не параллельна, а перпендикулярна плоскости орбиты Земли. Кроме того, размеры эллипса смещения звезды оказались больше ожидаемых (D на рис.214). В 1729 г. Брадлей объяснил это явление, получившее название аберрации света, как результат сложения скорости света, идущего от звезды, со скоростью орбитального движения Земли.

Если труба телескопа расположена на неподвижном небесном теле, то лучи света проходят через объектив телескопа Об и дают дифракционное изображение звезды в фокальной плоскости на оптической оси телескопа в точке F (рис.215-а).

Если телескоп расположен на движущейся Земле, а свет предоставляет собой поток корпускул (в 18 веке господствовала корпускулярная модель света), то пока свет распространяется в трубе телескопа от объектива Об к F, телескоп смещается на некоторое расстояние. В результате изображение звезды сместится из F в F¢. Чтобы изображение звезды вновь оказалось на оптической оси телескопа в точке F, телескоп надо наклонить в сторону движения Земли (рис.215-б).

Когда Земля находится в противоположных точках орбиты, телескоп наклоняется на угол j относительно направления на звезду то в одну сторону, то на такой же угол j в другую сторону. Если измерить угол 2j между максимальными отклонениями телескопа, то скорость света с найдётся из формулы: tgj = vtçct, Þ c = vçtgj. (26.4)

По измерениям Брадлея максимальный угол j = 20,5². Скорость v орбитального движения Земли была в то время уже известна, v » 30 км/с = 3·10⁴ м/с. Полагая для столь малых углов tgj = j (рад), получаем: c = 3,0∙10⁸ м/с.

Аберрация света обусловлена не фактом движения Земли, а изменением направления скорости этого движения. Если бы Земля равномерно двигалась по прямой, то аберрационные углы всех небесных светил были бы одинаковы и постоянны во времени. Поэтому они не обнаруживали бы себя.

5. Лабораторный метод Физо. Лабораторными называются методы, в которых источник и приёмник света находятся на Земле. Первый лабораторный опыт по измерению скорости света поставил в 1849 г. Ипполит Физо. Он, по сути, реализовал проект Галилея, автоматизировав процесс прерывания светового луча с помощью зубчатого колеса.

Свет от источника S идёт на полупрозрачное зеркало Зк, проходит между зубцами колеса К, отражается от зеркала М, вновь проходит между зубцами и сквозь полупрозрачное зеркало Зк попадает в глаз наблюдателя (рис.216).

Если колесо неподвижно, и свет проходит между зубцами в точке а, то глаз видит свет. При вращении колеса свет виден лишь тогда, когда за время его движения от а к М и обратно колесо успевает повернуться на один или несколько промежутков между зубцами. Так что возвращающийся луч снова попадает в промежуток.

Для измерений оказалось удобнее использовать полное затмение, когда возвращающийся луч попадает на зуб колеса. Если ширина щели равна ширине зубцов, то первое затмение наблюдается тогда, когда за время t = 2Lçc колесо повернётся на ширину зуба. Если Z – число зубцов, то для первого затмения справедливо 2Lçc=1çn ∙2Z, где ν – число оборотов в секунду.

Второе затмение будет наблюдаться при угловой скорости в 3 раза больше, третье затмение – при скорости в 5 раз больше, n-е затмение – при скорости в 2n – 1 раз больше. Поэтому для n-го затмения справедливо равенство , Þ . (26.5)

В опытах Физо установка имела следующие параметры: L = 8,633 км, Z = 720. Первое затмение наблюдалось при n = 12,6 с^–1. Отсюда скорость с = 4nLZ = 3,13·10⁸ м/с.

Число затмений n ограничивается прочностью механической части конструкции. В последующих опытах разных исследователей число n достигало трёх десятков. Использование для прерываний света вместо колеса ячейки Керра позволило уменьшить расстояние L до 3-х метров (Андерсен, 1937).

6. Лабораторный метод вращающегося зеркала Фуко. Идею вращающегося зеркала высказал Араго в 1838 г. В 1850 г. Леон Фуко реализовал её в своей установке. В 1862 г. с помощью этой установки Фуко измерил скорость света в воздухе (рис.217).

Свет от источника S проходит сквозь полупрозрачное зеркало Зк и линзу Л на вращающееся зеркало R. Отразившись от него, свет идёт на сферическое зеркало М, центр кривизны которого совпадает с осью вращения зеркала R. За время 2L/c, пока свет идёт от R к М и обратно, вращающееся зеркало R успевает повернуться на некоторый угол j. В результате отражённый от зеркала Зк зайчик О переместиться на расстояние l в положение O₁.

Если n – частота вращения зеркала R, то его угол поворота j = ω·t = 2πn ∙(2Lçc). С другой стороны, j = (lçb)/2, где b = SR – расстояние между источником света S и зеркалом R. Двойка в знаменателе здесь появляется потому, что угол поворота луча lçb в два раза больше угла j поворота зеркала. Приравниваем. j = 2pn ∙2Lçc =çlç2b, Þ c = 8pnLbçl. (26.6)

В опытах Фуко L = 20 м (Реальное расстояние MR составляло 4 м. Оно искусственно увеличивалось за счёт дополнительных зеркал. Поэтому L = 20 м есть эффективное расстояние), n достигало 800 Гц, b = 0,52 м, l = 0,7 мм. Отсюда с = 2,98∙10⁸ м/с.

Последующие опыты по измерению скорости света с, а их было выполнено разными исследователями несколько десятков, главной задачей ставили повышение точности определения величины с. В этом отношении выделяются опыты Майкельсона.

7. Метод вращающегося зеркала Майкельсона представляет собой развитие идеи вращающегося зеркала Фуко. Опыты по определению скорости света Альберт Майкельсон проводил с 1878 по 1931г. Рассмотрим схему последнего из них, начатого в 1926 г. (рис.218).

Эксперимент проводился в Калифорнии. Зеркало D было удалено от зеркала С на расстояние 35373,21 м. (Зеркала находились на горах Вильсон и Сан-Антонио. Определение с такой точностью расстояния между зеркалами само по себе представляет сложную триангуляционную задачу).

Зеркалом R служила восьмигранная стальная призма, вращавшаяся с частотой n. Принципиальным отличием в установке Майкельсона было то, что измерялось не смещение точки О, а подбиралась частота вращения n зеркала R такой, чтобы зайчик О оставался на месте. Это происходило в том случае, когда за время движения света от одной грани зеркала R до другой зеркало успевало повернуться точно на 1/8 оборота и принимало тождественное положение.

Измерения Майкельсона позволили получить самое точное для того времени значение скорости света. При n = 529,702 с^–1 получается с = 16nL = (299796 ± 4) км/с.

8. Измерение скорости света другими методами. После того, как было доказано, что свет – это электромагнитное излучение, появилась возможность измерения скорости света радиофизическими методами. Наиболее развит из них метод стоячих волн в полом цилиндрическом резонаторе. Зная длину волны излучения l, по резонансной частоте n определяется скорость света с = nl. Откачивая из резонатора воздух или заполняя его разными веществами, можно измерить скорость света как в вакууме, так и в разных средах.

Точность измерения величины с такими методами достигла в 70-х годах 20 века 11 знаков. По рекомендации Комиссии обозначений, единиц измерения и терминологии Международного совета теоретической и прикладной физики современное значение скорости света в вакууме принято равным с = (299792458 ± 1) м/с.

9. Роль скорости света в развитии физических теорий. Измерения скорости света сыграло важную роль в развитии физических теорий. В 19 веке они не только выполнили свою прямую задачу, но и дополнительно подтвердили волновую природу света.

В корпускулярной модели Ньютона скорость света в веществе должна быть больше скорости света в вакууме. Скорость световых частиц, переходящих из менее плотной среды более плотную, вследствие гравитационного притяжения более плотной средой должна, по Ньютону, увеличиваться. Поэтому показатель преломления, как видно из рис.219-а, в теории Ньютона есть отношение скорости света v₂ в более плотной среде к скорости света v₁ в менее плотной среде. 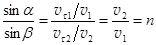, n > 1, v₂ > v₁. (26.7)

В волновой теории дело обстоит наоборот. Скорость света в веществе меньше скорости света в вакууме.

Действительно, если на рис.219-б ОА – волновой фронт в менее плотной среде 1 (вакуум), а СВ – волновой фронт в среде 2 (стекло), то луч в стекле пойдёт круче лишь при условии, что отрезок ОС меньше отрезка АВ.

Здесь АВ – расстояние, проходимое световой волной за время t в вакууме, АВ = v₁t. В течение этого времени t точка О волнового фронта ОА генерирует в среде 2 волну, распространяющуюся со скоростью v₂. Отрезок ОС = v₂×t.

Из геометрии рисунка следует 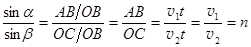, Þ v₁ > v₂. (26.8)

В 1850 г. Леон Фуко сравнил скорость света в воздухе v₁ со скоростью света в воде v₂. Для этого между зеркалами М и R в своей установке (рис.217) он располагал трубу с водой. Торцы трубы закрывались прозрачными стёклами. (Заметим, что первоначально установка была построена именно с целью сравнения скорости света в воде и в воздухе).

Результаты опытов Фуко показали, что скорость света в воде меньше скорости света в воздухе. Отношение скоростей оказалось равным v₁/v₂ = 4/3 = 1,33, что как раз и соответствует показателю преломления воды. Итак, чем оптически плотнее среда, тем меньше в ней скорость света. С максимальной скоростью свет распространяется в вакууме. Это явилось прямым доказательством справедливости волновой модели света.