ГЛАВА 9. КВАНТОВАЯ ОПТИКА

Тепловое излучение

1. Квантованность энергии. К концу 19 в. основанная на уравнениях Максвелла классическая электродинамика добилась больших успехов. Выяснилось, что – свет электромагнитные волны. Поэтому упразднилась эфирная гипотеза, а волновые свойства света стали вытекать из свойств электромагнитной волны. Законами электродинамики объяснились интерференция, дифракция, поляризация, дисперсия, рассеяние света.

Но к началу 20 в. выяснилось, что классическая электродинамика не может объяснить процессы испускания и поглощения света. Пытаясь объяснить связанные с этими процессами явления теплового излучения, фотоэффекта, спектральные закономерности и другие, Планк и Эйнштейн открыли свойство дискретности энергии испускаемого и поглощаемого излучения. В физику приходит идея дробности, квантованности энергии взаимодействия между объектами. Эта идея квантов оказалась очень плодотворной. Она существенно расширила и углубила физическую картину мира.

2. Тепловое излучение. Все случаи испускания света делятся на две группы.

а. Тепловое излучение. Оно испускается телами по причине их нагретости. Его испускают все тела выше абсолютного нуля.

б. Люминесцентное излучение. Оно не зависит так однозначно от температуры и может происходить в принципе и при абсолютном нуле.

Основное отличие этих видов излучения друг от друга в том, что тепловое излучение равновесно, а люминесцентное не равновесно.

Равновесность теплового излучения означает, что если нагретое тело поместить в замкнутую полость с идеально зеркальными стенками, то возвращаемая стенками энергия ЭМ волны будет поддерживать излучение и температуру нагретого тела сколь угодно долго.

Если же в полость с зеркальными стенками поместить люминесцирующее тело, то со временем процесс люминесцентного свечения иссякнет, хотя температура тела может повыситься. Например, поглощение гниющим деревом излучённых им в процессе хемилюминесценции ЭМ волны не приводит к восстановлению его органической ткани. Люминесцентное излучение прекратиться, как только израсходуется запасённая в ткани химическая энергия.

3. Спектральные величины. Они используются для описания процессов излучения и поглощения света. Таких величин две.

а. Спектральная светимость R_l связана с интегральной (полной) светимостью R соотношением: dR = R_ldl, или . (29.1)

Здесь R – полная светимость, то есть энергия излучения всех длин волн с единичной площадки в полупространстве. Единица R Вт/м².

Спектральная светимость R_l определяется отношением приращения светимости dR к ширине интервала длин волн dl, на котором это приращение произошло, R_l = dRçdl. Единица R_l Вт/м³.

б. Спектральный коэффициент поглощенияa_l есть отношение поглощённого потока Ф_погл излучения с длиной волны l в узком интервале длин волн dl к падающему потоку Ф_пад. . (29.2)

Т.е, величина a_l есть коэффициент поглощения света определённой длины волны l.

4. Модель абсолютно чёрного тела (АЧТ). Это понятие ввёл в 1859 Густав Кирхгоф для обозначения воображаемого тела, полностью поглощающего весь падающий на него свет независимо от длины волны. Для АЧТ а_l= 1 во всём интервале длин волн 0≤ l ≤∞.

АЧТ – это идеализация, модель, аналогичная материальной точке, абсолютно твёрдому телу и др.

Наилучшим практическим приближением к АЧТ является почти замкнутый сосуд с малым отверстием и непрозрачными стенками, имеющими одинаковую температуру во всех точках. Например, полый шар с малым отверстием, смещённым от центра к периферии (рис.227).

Луч, попавший в полость через отверстие, многократно отражается и при каждом отражении частично поглощается стенками полости. После нескольких отражений он поглощается практически полностью. В результате наружу данный луч не выходит. Это отверстие в стенке полости и есть модель поверхности АЧТ.

5. Законы теплового излучения. Их три.

а. Закон Кирхгофа, 1859 г. Отношение спектральной светимости R_λ любого тела к его спектральному коэффициенту поглощения а_l не зависит от природы тел и есть универсальная для всех тел функция длины волны l и температуры Т.

. Закон Кирхгофа, 1859 г. (29.3)

Так как коэффициент поглощения АЧТ а_l = 1, то закон Кирхгофа можно сформулировать ещё так: отношение спектральной светимости к коэффициенту поглощения любого тела равно спектральной светимости r_lTАЧТ.

Из закона Кирхгофа следует, что чем хуже поглощает тело электромагнитное излучение, тем меньше энергии излучает это тело по сравнению с АЧТ, имеющим ту же температуру. Все реальные тела в отличие от АЧТ называются в теории теплового излучения нечёрными. Для них а_l < 1.

У разных тел функция а_l имеет разный вид. Так как R_l = a_l r_lT, то это значит, что спектральный состав теплового излучения разных тел, имеющих одинаковую температуру, отличается между собой.

Если а_l тела постоянно во всём диапазоне 0≤l ≤∞, тело называется серым. Хотя серое тело излучает меньше энергии, чем АЧТ с той же температурой, спектральный состав их излучений одинаков (рис.228).

Свойство тел иметь отличное от АЧТ распределение интенсивности излучения по спектру (то есть по l) называется селективностью. У селективных излучателей коэффициент а_l меняется с изменением длины волны l. Вольфрам, например, имеет заметную селективность в видимой части спектра 400≤l≤800 нм. Максимум его излучения сдвинут в сторону более коротких длин волн. Поэтому вольфрам выгодно использовать в лампах накаливания.

б. Закон Стефана – Больцмана, 1884. В 1879 г. Йозеф Стефан экспериментально установил, что полная энергия, излучаемая нагретым телом, пропорциональна 4-й степени его абсолютной температуры.

Однако, при последующих измерениях выяснилось, что реальные тела не следуют точно этому закону. В 1884 г. Людвиг Больцман теоретически показал, что закон Стефана справедлив только для АЧТ. 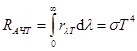. Закон Стефана – Больцмана (29.4)

Коэффициент σ называют постоянной Стефана – Больцмана. Из опыта найдено σ = 5,67×10^–8 Вт/(м²×К⁴).

Для нечёрных тел в общем случае R = АσТⁿ где А и n – некоторые функции температуры, А<1, n колеблется около 4.

в. Закон Вина, 1893 г. Вильгельм Вин на основе термодинамических соображений теоретически обосновал характер спектральной светимости АЧТ. Он нашёл, что r_lT есть произведение (сçl)⁵ на функцию от аргумента (сçlТ). Здесь с – скорость света в вакууме. Хотя вид функции f(cçlТ) установить не удалось, важно, что температура входит в неё в виде произведения lТ. Общий анализ функции f(cçlT) показал, что она имеет единственный максимум, удовлетворяющий условию:

l_max×T = Const = b. Закон смещения Вина (29.6)

Здесь l_max – это та длина волны, при которой функция r_lT имеет максимум при данной температуре Т.

Положение максимума функции спектральной светимости АЧТ по мере возрастания температуры смещается в сторону коротких длин волн. (Закон смещения Вина, рис.229).

Постоянная Вина b находится из опыта, b = 2,897×10^–3 м∙К.

6. Границы применимости тепловых законов. Хотя законы теплового излучения проверялись лишь для температур Т в несколько тысяч Кельвинов, теоретическое осмысление позволяет предположить, что эти законы справедливы и в области более высоких температур. Это значит, что разогретое до высоких температур вещество должно генерировать ЭМ излучение сколь угодно коротких длин волн. Так, из закона Вина следует, что при Т = 10⁵ К максимум излучения приходится на l_max = 30 нм (УФ диапазон), а при Т = 10⁸ К (термоядерный взрыв) l_max = 0,03 нм (рентгеновский диапазон).

7. Классическая теория теплового излучения. Теоретическое исследование теплового излучения имело основной целью определение вида функции спектральной светимости АЧТ r_lT. Излучение АЧТ моделировалось при этом как излучение полости модели АЧТ, в которой существовали стоячие ЭМ волны.

В июне 1900 г. Рэлей показал, что решение задачи о распределении энергии ЭМ поля в полости по частотам может быть сделано на основе гипотезы Больцмана о равномерном распределении энергии по степеням свободы. Он рассуждал примерно так.

Раз все стенки полости при любой температуре излучают ЭМ волны, то внутри полости существует ЭМ поле. Это поле можно разложить на системы стоячих ЭМ волн разных частот и направлений. При этом полагается, что на каждую монохроматическую волну приходится средняя энергия = kT, где kTç2 – энергия электрического поля, и kTç2 – энергия магнитного поля. В результате для спектральной светимости АЧТ Рэлей получил формулу:

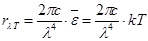. Формула Рэлея-Джинса, 1900 (29.7)

Здесь с – скорость света в вакууме, k – постоянная Больцмана. В 1909 г. эту формулу более строго обосновал Джеймс Джинс. Поэтому функцию r_lT распределения энергии в спектре излучения АЧТ, полученную в рамках электромагнитной теории света, называют формулой Рэлея – Джинса.

Формула Рэлея – Джинса удовлетворяет опыту лишь в области длинных волн (рис.230). Но в области коротких волн из неё следует абсурдный результат: энергия излучения нагретого тела с уменьшением длины волны l неограниченно возрастает (в формуле 29.7 l в знаменателе). Поэтому тела могут находиться только при температуре абсолютного нуля. При малейшем нагревании они должны были бы излучать бесконечно большую энергию в коротковолновой области спектра. Этот противоречащий опыту вывод Пауль Эренфест назвал ультрафиолетовой катастрофой.

То, что последовательный в рамках классической электродинамики вывод противоречит опыту, говорит о том, что в тепловом излучении есть закономерности, не объяснимые в рамках классической физики.

8. Квантовая теория теплового излучения. В декабре 1900 г. Макс Планк предложил решить проблему излучения АЧТ с помощью гипотезы о дискретных порциях энергии – квантах. Согласно концепции Планка, атом, испускающий или поглощающий свет, нельзя рассматривать как классический осциллятор, способный непрерывно изменять свою энергию. Энергия колебательного движения каждого атома может принимать, по Планку, дискретный ряд значений: e = nhn, где n = 0,1,2,..., hn - кванты энергии, которыми могут обмениваться атомы. Величина кванта энергии пропорциональна частоте излучения n. Коэффициент h – новая фундаментальная постоянная, введённая Планком. Её размерность называют действием, h = 6,62×10^–34 Дж×с.

Если предположить, что распределение атомов по энергиям подчиняется закону Больцмана n = n₀ exp(–eçkT), то, как показал Планк, среднее значение энергии таких квантовых осцилляторов в ансамбле определяется формулой:

. Формула Планка, 1900 (29.8)

(Вывод формулы Планка см.: Конспект лекций, Часть 2, Тепл. и молек. Физика, §21, с.с. 70-73). Подставив планковское выражение (29.8) для в формулу Рэлея – Джинса (29.7), получаем: 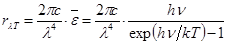. (29.9)

Посмотрим, каковы возможности формулы (29.9) в объяснении опытных и теоретических закономерностей.

а. Прогноз Вина о виде функции r_lT. Подставим в формулу спектральной све-тимости АЧТ (29.9) n = сçl. . (29.10)

Квантовая формула для r_lT полностью соответствует прогнозу Вина (формуле 29.5).

б. Закон Стефана – Больцмана. Вычислим полную светимость АЧТ, используя подстановку hcçklT = x. Отсюда l = hcçkTx, dl = – (hcçkT)×dxçx². (29.11)

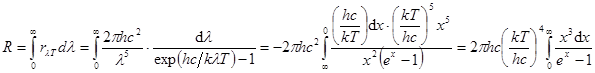(29.12)

(Поменяв местами пределы интегрирования, мы изменим знак перед интегралом.) Интеграл Пуассона в выражении равен p ⁴ç15. Итак, . (29.13)

Коэффициент перед Т ⁴ есть комбинация констант. Его вычисление даёт:

.

Из формулы Планка вытекает закон Стефана Больцмана.

в. Закон Вина. Чтобы найти максимум спектральной светимости АЧТ, надо исследовать функцию r_lT на экстремум по l. Если выбрать подстановку z = klT/hc, пропорциональную l, то точки экстремума по z и по l совпадут. Тогда

, (29.14)

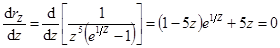. (29.15)

Это трансцендентное уравнение. Его корни нельзя выразить в виде алгебраического выражения. Они находятся численными методами, z_max= kl_maxTçhc = 0,2014. Откуда имеем м∙К, что соответствует закону Вина.

г. Формула Рэлея – Джинса получается из квантовой формулы спектральной светимости как предельный случай при больших l, если в формуле Планка (29.8) показатель степени экспоненты не более 0,1, hcçklT ≤ 0,1, то экспоненту можно разложить в ряд и ограничиться двумя первыми членами. Exp(hcçklT) = 1 + hcçklT + ... (29.15)

Подставив в формулу (29.8), получаем: 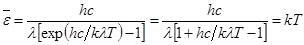. (29.16)

Подставив это значение в общее выражение Рэлея (29.7), получаем формулу Рэлея – Джинса. Чтобы определить, с каких значений длин волн l квантовая формула переходит в формулу Рэлея – Джинса, из выражения корня трансцендентного уравнения z_max = kl_max×Tçhc выразим hcçkT = l_maxçz_max и подставим в показатель экспоненты.

, Þ 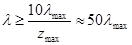. (29.17)

При l = 50l_max относительная погрешность формулы Рэлея – Джинса составляет 5,1%, а с ростом l она уменьшается.

9. Пирометрия (от греч. рyr -огонь) – бесконтактное измерение температуры тел на основе законов теплового излучения. В зависимости от методов измерения различают три вида температур.

а. Радиационная температура определяется через полный тепловой поток с использованием закона Стефана - Больцмана.

Допустим, тело имеет светимость R. Если неизвестен коэффициент поглощения тела А, то остаётся уподобить это тело АЧТ. Тогда

R = sT⁴, Þ . (29.17)

Если тело серое (а_l = Сonst) и его коэффициент поглощения А = а_l известен, то

R = AsT⁴, Þ . (29.18)

В этом случае измеряемая радиационная температура близка к истинной.

б. Яркостная температура определяется наиболее часто. В этом случае излучение нагретого тела сравнивается с излучением АЧТ в узком интервале длин волн по яркости их поверхностей. Обычно в яркостных пирометрах используется красный светофильтр с длиной волны пропускания l = 660 нм. Пирометр предварительно градуируется по АЧТ.

Равенство температур фиксируется визуально сравнением яркости светящейся проволоки прибора с яркостью светящегося объекта (рис.231). Температуры тел считаются одинаковыми, когда они визуально сливаются.

Если тело серое, и его коэффициент поглощения а_l известен, то по яркостной температуре Т_ярк, измеренной пирометром, можно определить истинную, . (29.19)

Яркостная температура измеряется обычно до 5000 °С. Поэтому длина волны светофильтра l находится в области максимума спектральной светимости или несколько левее (рис.232).

в. Цветовая температура. В основу метода её измерения положен закон смещения Вина l_maxТ = b. Это температура АЧТ, при которой максимум в его излучении приходится на ту же длину волны l_max, что и в излучении реального тела. Для измерения цветовой температуры надо построить кривую спектральной светимости и найти по ней длину волны l_max, соответствующую максимуму.

Например, максимум спектральной светимости в излучении Солнца приходится на l_max= 470 нм. Из формулы Вина находим цветовую температуру. T = bçl_max= 6,15∙10³ K.

Цветовая температура также применима лишь к серым телам, распределение энергии в спектре которых мало отличается от АЧТ.