Уравнения в полных дифференциалах
Однородные уравнения первого порядка
Функция 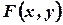 называется однородной степени
называется однородной степени 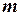 , если для любых
, если для любых 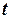 выполняется тождество
выполняется тождество
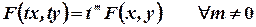
Дифференциальное уравнение первого порядка
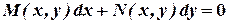
называется однородным, если 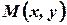 и
и 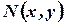 - однородные функции одной и той же степени.
- однородные функции одной и той же степени.
С помощью новой переменной 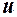 , вводимой по формуле
, вводимой по формуле
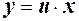
однородное уравнение приводится к уравнению с разделяющимися переменными.
Пример. Проинтегрировать уравнение 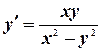 .
.
Введем новую переменную 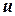 по правилу
по правилу 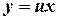 , получим
, получим
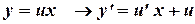
Подставим в исходное уравнение:
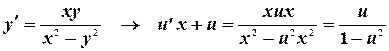
Преобразуем
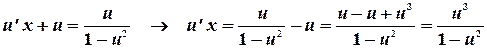
Перепишем получившееся уравнение в виде:
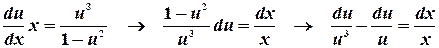
Проинтегрируем левую и правую части:
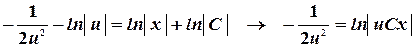
Вернемся к "старым" переменным:
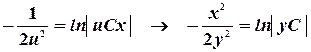
Линейные уравнения
Уравнение вида
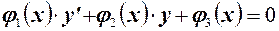
или

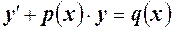
называется линейным дифференциальным уравнением первого порядка.
Решение линейного уравнения ищут в виде произведения двух функций
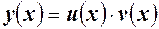
Следовательно,
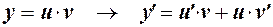
Подстановка выражений для 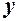 и
и 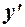 в исходное уравнение приводит его к виду
в исходное уравнение приводит его к виду
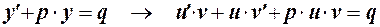
Отсюда
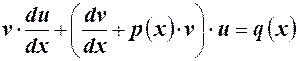
Это уравнение приводят к более простому виду, полагая выражение в круглых скобках равным нулю:
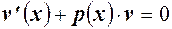
Тем самым мы получаем уравнение для определения 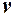 .
.
Тогда функция 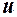 определяется уравнением
определяется уравнением
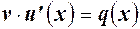 .
.
Пример.
Проинтегрировать дифференциальное уравнение
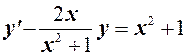 .
.
Данное уравнение является линейным. Решение ищем в виде 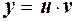 . Найдем производную от этого выражения:
. Найдем производную от этого выражения: 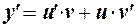 . Значения
. Значения 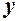 и
и 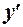 подставим в исходное уравнение:
подставим в исходное уравнение:
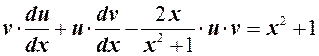
Перегруппируем его
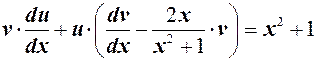
В качестве 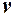 выбираем одну из функций, обращающих в нуль коэффициент при
выбираем одну из функций, обращающих в нуль коэффициент при 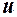 - круглую скобку:
- круглую скобку:
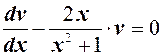
Разделив переменные, получим
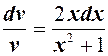
Откуда
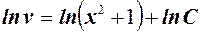
Или, после операции потенцирования:
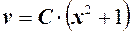 .
.
Не теряя общности, положим 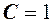 . Отсюда получаем выражение для
. Отсюда получаем выражение для 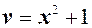 .
.
Для определения 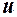 остается уравнение
остается уравнение
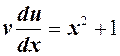
Подставив сюда найденное значение 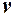 , получим:
, получим:
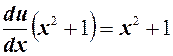 , или
, или 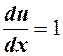
из которого определяем 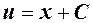 . Соответственно, общее решение будет иметь вид:
. Соответственно, общее решение будет иметь вид:
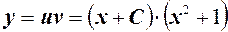
Также можно воспользоваться методом вариации произвольной постоянной, который состоит в следующем. Сначала находят общее решение соответствующего однородного уравнения 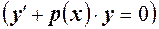 . Далее величину
. Далее величину 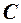 , входящую в это уравнение, полагают функцией
, входящую в это уравнение, полагают функцией 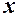 и находят ее.
и находят ее.
Уравнение Бернулли
Уравнением Бернулли называется уравнение вида
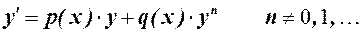
Решение.
1. Можно интегрировать это уравнение как линейное, полагая, как и ранее, 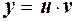 . Отсюда
. Отсюда 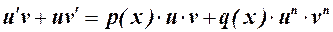 .
.
Решая его, получим:
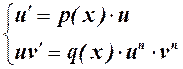
2. Это уравнение сводится к линейному, если разделить его на 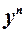 :
:
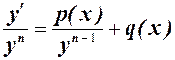
Делаем замену
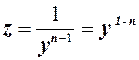 .
.
Продифференцировав замену, найдем что
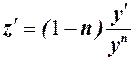 .
.
Или
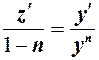 .
.
Подставляя в исходное уравнение, получим
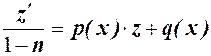
которое является линейным дифференциальным уравнением первого порядка.
Пример. Проинтегрировать уравнение 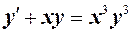 .
.
Введем переменную 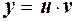 . Найдя производную и подставив ее в исходное уравнение, получим:
. Найдя производную и подставив ее в исходное уравнение, получим:
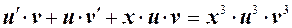
или
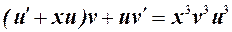 .
.
Это уравнение распадается на два 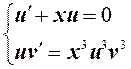 .
.
Решаем первое
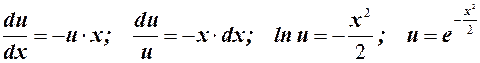
Решаем второе
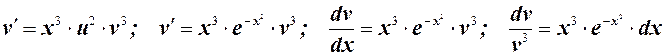
Интегрируем правую часть:
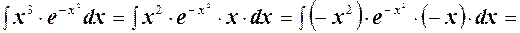
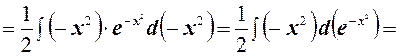
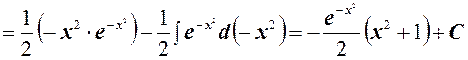
Отсюда
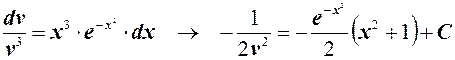 .
.
В результате получим
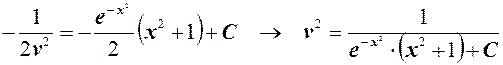 .
.
В итоге
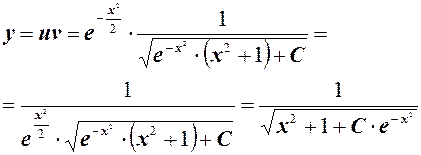
Уравнения в полных дифференциалах
Уравнением в полных дифференциалах называется уравнение
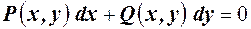
левая часть, которого является полным дифференциалом некоторой функции, т.е.
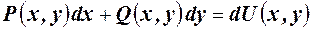
Общий интеграл уравнения определяется формулой
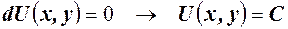 .
.
Далее, поскольку
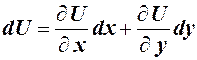
то из условия 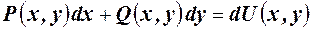 следуют уравнения
следуют уравнения
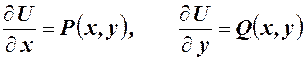
которыми определяется функция 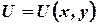 . Необходимое и достаточное условие того, что уравнение является уравнением в полных дифференциалах, выражается равенством
. Необходимое и достаточное условие того, что уравнение является уравнением в полных дифференциалах, выражается равенством
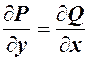
которое вытекает из условия равенства смешанных производных:
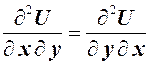 .
.
Если левая часть исходного уравнения не является полным дифференциалом, но становится таковым при умножении на некоторую функцию 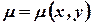 -
- 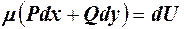 , то
, то 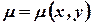 называется интегрирующим множителем.
называется интегрирующим множителем.
Интегрирующий множитель зависит только от 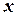 , т.е.
, т.е. 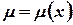 , если
, если
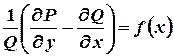
и зависит только от 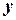 , если
, если
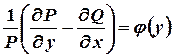
Пример. Проинтегрировать уравнение 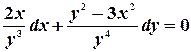 .
.
Имеем 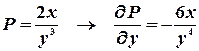 ,
, 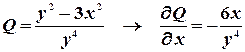 .
.
Мы видим, что 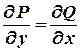 и, следовательно, это уравнение – дифференциальное уравнение в полных дифференциалах.
и, следовательно, это уравнение – дифференциальное уравнение в полных дифференциалах.
Поэтому 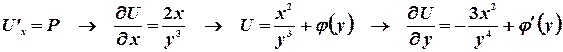 .
.
Аналогично
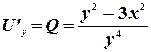 .
.
Сравнивая с найденным, запишем:
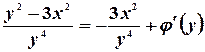 .
.
Отсюда вытекает, что
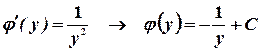
Отсюда
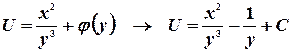 .
.
Следовательно, интеграл уравнения имеет вид:
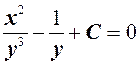 .
.
Дата добавления: 2020-05-20; просмотров: 519;











