Линейные неоднородные дифференциальные уравнения второго
порядка с постоянными коэффициентами
Если 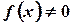 , то уравнение будет иметь вид:
, то уравнение будет иметь вид:
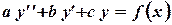
и называться линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Это уравнение может быть приведено к виду
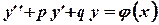
Общее решение этого уравнения определяется формулой
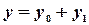
где 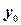 - общее решение соответствующего однородного уравнения
- общее решение соответствующего однородного уравнения
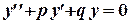 ,
,
а 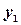 - частное решение исходного уравнения
- частное решение исходного уравнения 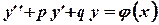 .
.
В простейших случаях, когда функция 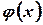 является показательной, или многочленом, указанное частное решение находится с помощью метода неопределенных коэффициентов.
является показательной, или многочленом, указанное частное решение находится с помощью метода неопределенных коэффициентов.
1. Если
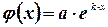
где 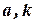 - постоянные, то частное решение ищут в виде
- постоянные, то частное решение ищут в виде
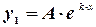 ,
,
когда 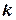 не является корнем характеристического уравнения или в виде
не является корнем характеристического уравнения или в виде
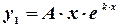 ,
,
когда 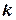 - простой корень характеристического уравнения, или
- простой корень характеристического уравнения, или
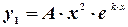 ,
,
когда 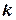 - кратный корень указанного уравнения.
- кратный корень указанного уравнения.
2. Если
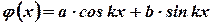
где 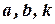 - постоянные, то частное решение ищут в виде
- постоянные, то частное решение ищут в виде
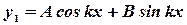 ,
,
когда 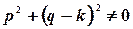 , и в виде
, и в виде
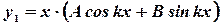 ,
,
когда 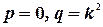 .
.
3. Если
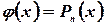 ,
,
где 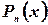 - многочлен степени
- многочлен степени 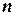 , то частное решение дифференциального уравнения
, то частное решение дифференциального уравнения 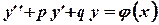 ищут в виде
ищут в виде
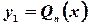
в случае, когда 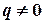 , и в виде
, и в виде
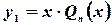 ,
,
когда 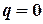 ,
, 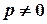 .
.
Пусть дано неоднородное уравнение
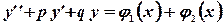
правая часть которого есть сумма двух функций 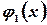 и
и 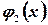 .
.
Если 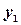 является частным решением
является частным решением 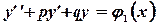 , а
, а 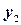 - частным решением
- частным решением 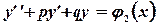 , то
, то 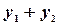 - частное решение
- частное решение 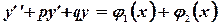 .
.
Пример. Проинтегрировать уравнение 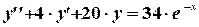 .
.
Найдем сначала общее решение соответствующего однородного уравнения
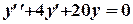 .
.
Характеристическое уравнение 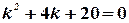 имеет корни
имеет корни
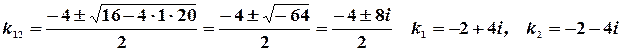
Следовательно, общее решение однородного уравнения определяется формулой
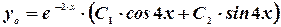 .
.
Переходим к отысканию частного решения исходного уравнения.
Так как в данном случае 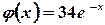 (т.е. имеет вид
(т.е. имеет вид 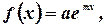 где
где 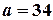 ,
, 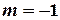 ) и
) и 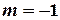 не является корнем характеристического уравнения, то частное решение ищем в виде
не является корнем характеристического уравнения, то частное решение ищем в виде
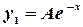 .
.
Найдя производные этой функции
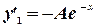 и
и 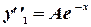 ,
,
и подставляя выражения для 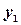 ,
, 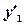
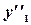 в исходное уравнение, получаем
в исходное уравнение, получаем
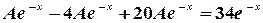 .
.
Так как 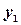 - решение уравнения, то последнее равенство выполняется для всех
- решение уравнения, то последнее равенство выполняется для всех 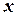 , т.е. является тождеством:
, т.е. является тождеством:
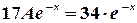
откуда 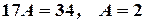 . Следовательно, частное решение имеет вид
. Следовательно, частное решение имеет вид
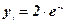 .
.
Соответственно, общее решение
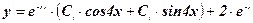 .
.
Дата добавления: 2020-05-20; просмотров: 471;











