Дифференциальные уравнения второго порядка.
Дифференциальным уравнением второго порядка называется уравнение относительно искомой функции, ее первой и второй производной. В общем виде это уравнение записывается как
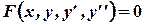
где 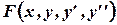 заданная функция указанных аргументов.
заданная функция указанных аргументов.
Общим решением дифференциального уравнения второго порядка называется функция 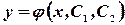 от
от 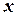 и двух независимых произвольных постоянных
и двух независимых произвольных постоянных 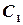 и
и 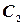 , обращающих данное уравнение в тождество. Общее решение, заданное в неявном виде
, обращающих данное уравнение в тождество. Общее решение, заданное в неявном виде 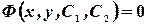 , называют общим интегралом.
, называют общим интегралом.
Частным решением уравнения 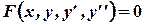 называется решение
называется решение 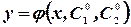 , полученное из общего путем фиксирования значений произвольных постоянных:
, полученное из общего путем фиксирования значений произвольных постоянных: 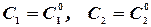 .
.
Задача Коши. Найти решение 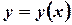 дифференциального уравнения второго порядка, удовлетворяющее условиям:
дифференциального уравнения второго порядка, удовлетворяющее условиям: 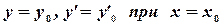 . Числа
. Числа 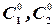 , определяющие искомое частное решение, находятся из системы уравнений:
, определяющие искомое частное решение, находятся из системы уравнений:
 .
.
9. Уравнения 2-го порядка, допускающие понижение порядка.
Если уравнение 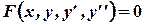 разрешимо относительно старшей производной, то его можно представить в виде
разрешимо относительно старшей производной, то его можно представить в виде
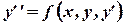 .
.
К простейшим интегрируемым дифференциальным уравнениям второго порядка относятся уравнения, для которых функция, стоящая в правой части зависит только от одного из трех аргументов
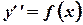 (А)
(А)
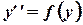 (Б)
(Б)
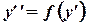 (В)
(В)
Общее решение уравнения (А) находится двукратным интегрированием.
Уравнения (Б) (В) интегрируются подстановкой

которая дает возможность свести их к уравнениям с разделяющимися переменными
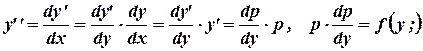
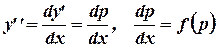
Уравнение 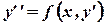 , подстановкой
, подстановкой  приводится к уравнению первого порядка
приводится к уравнению первого порядка 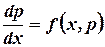 , в котором роль независимой переменной играет
, в котором роль независимой переменной играет 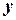 .
.
Пример.
Проинтегрировать дифференциальное уравнение:
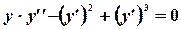 .
.
Делаем замену  . Отсюда
. Отсюда
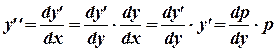 .
.
В результате исходное уравнение примет вид
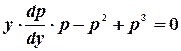 .
.
Преобразуем его следующим образом:
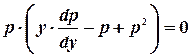 .
.
Это уравнение распадается на два.
1. 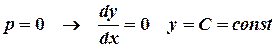
2. 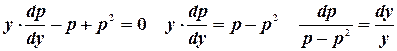 .
.
Используя, что 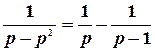 , найдем:
, найдем:
3. 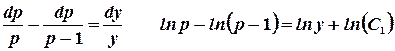 .
.
Или 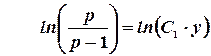 . Отсюда
. Отсюда
4. 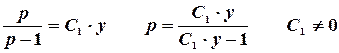 . Возвращаемся к старой переменной.
. Возвращаемся к старой переменной.
5. 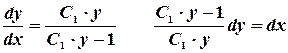 . Интегрируем.
. Интегрируем.
6. 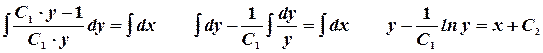
Дата добавления: 2020-05-20; просмотров: 493;











