Умозаключения по логическому квадрату

Прежде чем рассматривать умозаключения по логическому квадрату, обратимся к самому понятию логического квадрата. Это понятие связывают с именем византийского логика Михаила Пселла, жившего в 11 в. Логический квадрат представляет собой диаграмму, служащую для выражения и запоминания отношений между четырьмя видами категорических суждений – общеутвердительными, общеотрицательными, частноутвердительными и частноотрицательными. Он является примером мнемонических средств, которые широко использовались в философии и науке средних веков[2].

Нарисуем квадрат, соединив его вершины диагоналями и расположив в них следующим образом символы категорических суждений:

A E

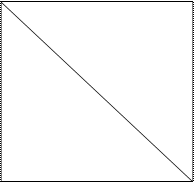I O

Между категорическими суждениями, связанными на нашей диаграмме отрезками прямых, существуют различные отношения:

1. между суждениями A и O, а также E и I – отношение противоречия;

2. между суждениями A и E – отношение противоположности;

3. между суждениями I и O – отношение субконтрарности;

4. между суждениями A и I, а также E и O – отношений следования.

Отношение противоречия (или контрадикторности) характеризуется тем, что связанные им суждения не могут быть вместе истинными и не могут быть вместе ложными. Эти суждения называются противоречащими (или контрадикторными). Если одно из них истинно, то другое ложно, а если одно из них ложно, то другое истинно. Отношение противоречия существует, например, между суждениями «Все коммерческие организации платят налог на прибыль» (A) и «Некоторые коммерческие организации не платят налог на прибыль» (O), а также между суждениями «Ни одна некоммерческая организация не платит налог на прибыль» (E) и «Некоторые некоммерческие организации платят налог на прибыль» (I).

Отношение противоположности (или контрарности) характеризуется тем, что связанные им суждения не могут быть вместе истинными, но могут быть вместе ложными. Эти суждения называются противоположными (или контрарными). Если одно из них истинно, то другое ложно, а если одно из них ложно, то другое может быть как истинным, так и ложным. Отношение противоположности существует, например, между суждениями «Все коммерческие организации платят налог на прибыль» (A) и «Ни одна коммерческая организация не платит налог на прибыль» (E).

Отношение субконтрарности (или подпротивности) характеризуется тем, что связанные им суждения не могут быть вместе ложными, но могут быть вместе истинными. Эти суждения называются субконтрарными (или подпротивными). Если одно из них ложно, то другое истинно, а если одно из них истинно, то другое может быть как истинным, так и ложным. Отношение субконтрарности существует, например, между суждениями «Некоторые коммерческие организации платят налог на прибыль» (I) и «Некоторые коммерческие организации не платят налог на прибыль» (O).

Отношение следования характеризуется тем, что истинность общего суждения влечёт за собой истинность частного суждения того же самого качества, но истинность частного суждения не влечёт за собой истинность общего суждения того же самого качества. Если общее суждение истинно, то частное суждение того же самого качества также истинно, а если частное суждение истинно, то общее суждение того же самого качества может быть как истинным, так и ложным. Отношение следования существует, например, между суждениями «Все коммерческие организации платят налог на прибыль» (A) и «Некоторые коммерческие организации платят налог на прибыль» (I), а также между суждениями «Ни одна некоммерческая организация не платит налог на прибыль» (E) и «Некоторые некоммерческие организации не платят налог на прибыль» (O).

Охарактеризовав отношения между категорическими суждениями, обратимся к рассмотрению умозаключений по логическому квадрату. Умозаключение по логическому квадрату представляет собой непосредственное умозаключение, в котором заключение выводится из посылки на основании отношений между категорическими суждениями. Мы можем сформулировать для него 14 принципов правильного умозаключения, обоснование которых предполагает ссылку на отношения между категорическими суждениями:

Отношение противоречия

1. Если A истинно, то O ложно

2. Если A ложно, то O истинно

3. Если O истинно, то A ложно

4. Если O ложно, то A истинно

5. Если E истинно, то I ложно

6. Если E ложно, то I истинно

7. Если I истинно, то E ложно

8. Если I ложно, то E истинно

Отношение противоположности

9. Если A истинно, то E ложно

10. Если E истинно, то A ложно

Отношение субконтрарности

11. Если I ложно, O истинно

12. Если O ложно, то I истинно

Отношение следования

13. Если A истинно, то I тоже истинно

14. Если E истинно, то O тоже истинно

Иногда выводить заключения из посылок с помощью умозаключений по логическому квадрату проще, чем с помощью умозаключений посредством преобразования суждений. Так, мы знаем, что все коммерческие организации должны платить налог на прибыль. Но как мы можем сделать естественный вывод, что и некоторые из этих организаций должны платить налог на прибыль? Иными словами, как применить общее правило к частному случаю? Если обратиться к умозаключению посредством обращения, то получить нужное нам заключение «Некоторые коммерческие организации должны платить налог на прибыль» мы сможем не сразу, а только в два шага. Действительно, на первом шаге мы используем умозаключение

Все коммерческие организации должны платить налог на прибыль. Следовательно, некоторые из тех организаций, которые должны платить налог на прибыль, являются коммерческими,

а на втором – умозаключение

Некоторые из тех организаций, которые должны платить налог на прибыль, являются коммерческими. Следовательно, некоторые коммерческие организации должны платить налог на прибыль,

заключением которого является как раз суждение «Некоторые коммерческие организации должны платить налог на прибыль». Однако с помощью умозаключения по логическому квадрату мы можем получить это суждение сразу, выведя его из посылки «Все коммерческие организации должны платить налог на прибыль».

[1] Умозаключения, исследование которых Аристотелем положило начало логике как науке, называются дедуктивными. Френсис Бэкон, живший в Новое время, противопоставил дедуктивным умозаключениям индуктивные, которые широко используются в естественных науках. Посылки индуктивного умозаключения содержат знание о части предметов некоторого класса, однако его заключение касается уже всех предметов, т. е. выходит за рамки информации, содержащейся в посылках. Мы придерживаемся точки зрения, согласно которой индуктивные умозаключения являются предметом изучения не логики, а методологии

[2] Прилагательное «мнемонический» производно от существительного «мнемоника» (гр. «mnemonika»), означающего «искусство запоминания».