Затем из каждого оставшегося уравнения вида
Методы решения систем линейных алгебраических уравнений (СЛАУ)
Две группы методов-точные и приближенные.
Точные (прямые) - позволяют получить точное решение с помощью конечного числа арифметических действий.
Приближенные- позволяют получить точное решение с помощью бесконечного числа арифметических действий.
Известные точные методы- Крамера, Гаусса (метод Крамера в вычислительной практике не используется из-за большого количества вычислений).
Метод Гаусса
Данный метод также называется методом последовательного исключения неизвестных. Он относится к группе прямых методов и основан на преобразовании исходной системы к эквивалентной форме с треугольной матрицей коэффициентов.
Исходная система
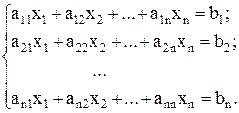 (1)
(1)
или A*x=B(в матричном виде)
При использовании метода Гаусса задача решается в два этапа:
1) прямой ход;
2) обратный ход.
Прямой ход заключается в преобразовании системы к треугольному виду.
При обратном ходе производится вычисление значений неизвестных.
Прямой ход метода Гаусса. Для получения расчетных формул прямого хода преобразуем исходную систему (1), заменив элементы bi ( 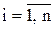 ) на ai,n+1. В результате система (1) будет иметь следующий вид
) на ai,n+1. В результате система (1) будет иметь следующий вид
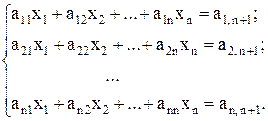
Прямой ход выполняется за (n-1) шагов, причем на каждом шаге из уравнений с номерами k + 1, k + 2, …, n исключается неизвестное xk.
На первом шаге сначала первое уравнение делится на a11 ¹ 0. Получим
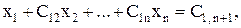 (3)
(3)
где 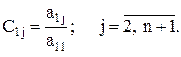
Затем из каждого оставшегося уравнения вида
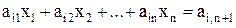 (
( 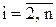 )
)
вычитается полученное уравнение (3), умноженное на коэффициент ai1. В итоге, после выполнения первого шага прямого хода система уравнений примет следующий вид
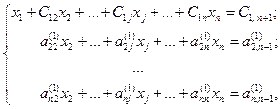 (4)
(4)
где
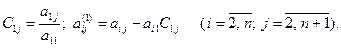
На втором шаге указанные выше действия повторяются над (n - 1) уравнениями системы (4), всеми кроме первого, с целью исключения переменной x2, где 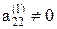 .
.
В итоге получим
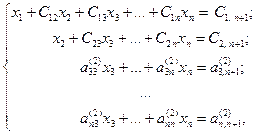
где
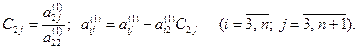
Повторяя шаги прямого хода (n - 1) раз, окончательно получим систему уравнений треугольного вида
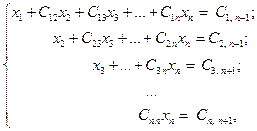 (5)
(5)
где
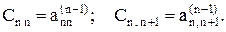
Обратный ход метода Гаусса. После приведения исходной системы уравнений (1) к треугольному виду (5) вычисляются значения корней по следующим формулам
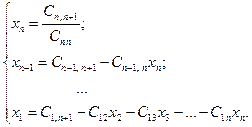
Таким образом, расчетные формулы обратного хода имеют вид
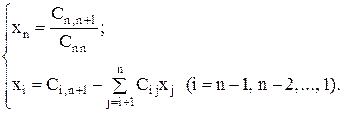
Дата добавления: 2020-05-20; просмотров: 509;











