Метод итераций (Якоби).
Пусть дана система линейных уравнений
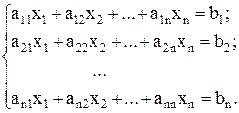
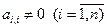 .
.
Тогда переменную x1 можно выразить из первого уравнения, 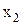 - из второго уравнения и т. д.
- из второго уравнения и т. д.
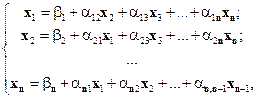 (10)
(10)
где 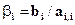 и
и 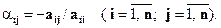
Система (10) называется системой линейных уравнений, приведенной к нормальному виду. Матричная форма записи такой системы представляется как
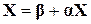 (11)
(11)
где
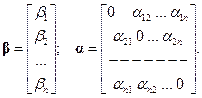
При решении системы (11) за нулевое приближение корней может быть принят столбец свободных членов, т.е. 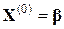 . Любое k-е приближение (
. Любое k-е приближение ( 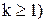 вычисляется по формуле
вычисляется по формуле
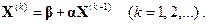
Если последовательность приближений 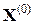 ,
, 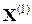 ,
, 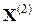 , ...,
, ..., 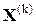 , ... имеет предел
, ... имеет предел 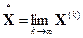 , то этот предел является точным решением системы уравнений (2).
, то этот предел является точным решением системы уравнений (2).
К сожалению метод итераций имеет условную сходимость. Условие сходимости
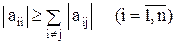 (12)
(12)
Иначе говоря в каждой строке системы модули диагональных элементов должны быть больше суммы модулей остальных элементов. Добиться выполнения данного условия можно, например, поменяв местами строки системы.
Вычисления продолжаются до тех пор, пока значения 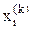 не станут достаточно близкими к
не станут достаточно близкими к 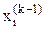
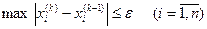 (13)
(13)
где e - некоторое положительное число, характеризующее погрешность определения корней системы уравнений.
Иногда для контроля точности используют невязки (ведут вычисления до достижения минимальных невязок)
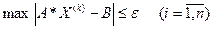 (14)
(14)
Достоинства и недостатки метода итераций
Достоинства
1. Простота.
2. Отсутствие накопления погрешностей.
Недостатки
1. Довольно большое количество итераций(низкая скорость сходимости).
2.Условная сходимость.
Метод Зейделя
Метод Зейделя представляет собой модификацию метода итераций. В нем при определении значения переменной 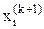 на некоторой (k+1)-ой итерации используются только что вычисленные (k+1)-е приближения неизвестных
на некоторой (k+1)-ой итерации используются только что вычисленные (k+1)-е приближения неизвестных 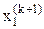 ,
, 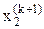 , ...,
, ..., 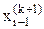 .
.
Пусть дана система уравнений (10). Выбранные начальные приближения корней 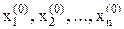 подставляются в первое уравнение
подставляются в первое уравнение
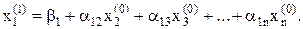
Для определения 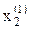 полученное значение
полученное значение 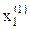 сразу же подставляется во второе уравнение системы
сразу же подставляется во второе уравнение системы
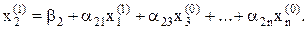
Аналогично определяются приближения корней 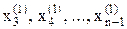 . Значение
. Значение 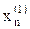 вычисляется с использованием первых приближений всех переменных
вычисляется с использованием первых приближений всех переменных 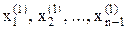 как
как
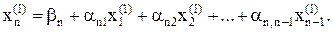
Как правило, процесс в методе Зейделя сходится к единственному решению быстрее, чем при использовании метода Якоби.
Метод релаксации
Простейшее объяснение метода релаксации следующее. Практически все итерационные методы характеризуются следующим рекуррентным соотношением
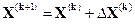 ,
,
где 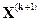 ,
, 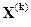 -результаты последующей и предыдущей итераций;
-результаты последующей и предыдущей итераций;
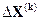 -некоторые приращения, зависящие от применяемого метода. В методе релаксации эти приращения умножаются на некоторую константу
-некоторые приращения, зависящие от применяемого метода. В методе релаксации эти приращения умножаются на некоторую константу 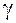 , называемую параметр релаксации, то есть
, называемую параметр релаксации, то есть
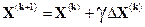 . (14)
. (14)
Теоретически 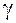 изменяется от 0 до 2, при
изменяется от 0 до 2, при 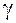 >1-это метод верхней релаксации, при
>1-это метод верхней релаксации, при 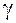 <1-соответственно метод нижней релаксации.
<1-соответственно метод нижней релаксации.
В неявном виде методы Якоби и Зейделя описываются выражением
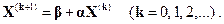
Для явного выражения приращений вычтем из обеих частей
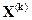 . Тогда
. Тогда
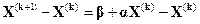
Или
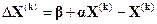 (15)
(15)
Тогда
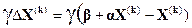 (15)
(15)
Подставив (15) в (14) после преобразований окончательно получим
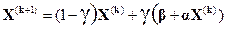
В большинстве случаев параметр 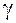 определяется опытным путем из условия минимума итераций. На практике метод релаксаций часто (но не всегда) позволяет резко снизить количество итераций.
определяется опытным путем из условия минимума итераций. На практике метод релаксаций часто (но не всегда) позволяет резко снизить количество итераций.
Пример реализации изложенных методов в среде Mathcad
Исходная система в матричной форме Ax=B
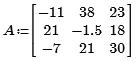
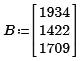
Дата добавления: 2020-05-20; просмотров: 604;











