Анализ каскада с общим эмиттером
ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ УСИЛИТЕЛЕЙ НА БИПОЛЯРНЫХ ТРАНЗИСТОРАХ
Рассмотренный ранее анализ параметров усилителей на биполярных транзисторах не учитывал целый ряд факторов, который необходимо учитывать при их определении и анализе. К этим факторам следует отнести наличие дополнительных элементов в схеме, обеспечивающих задание необходимых параметров рабочей точки, и элементов обеспечивающих связь между источником сигнала и нагрузкой по переменному току. На рис.2.30 показана схема с общим эмиттеров, в которой рабочая точка задается напряжением на базе с помощью резисторов R1, R2. Связь на переменном токе с источником и нагрузкой осуществляется с помощью конденсаторов Cвх и Cвых .
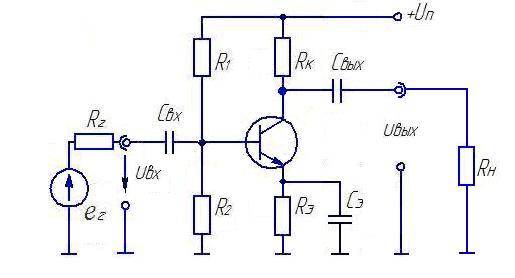
Рис.2.30. Усилительный каскад с общим эмиттером
Резисторы базового делителя на переменном токе уменьшают входное сопротивление каскада rвхк до значения
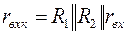 ,
,
где rвх – входное сопротивление каскада между базой и общим проводом, выражения для определения которого получены в предыдущих лекциях.
При анализе частотных свойств коэффициента усиления каскада по напряжению необходимо учитывать наличие в схемах замещения каскада разделительных конденсаторов Свх и Свых, конденсатора Cэ шунтирующего резистор в цепи эмиттера Rэ, а также емкости переходов транзистора, из которых наиболее существенное влияние на частотные свойства оказывает барьерная емкость перехода база-коллектор Сбк . Так на нижних частотах возрастает сопротивление разделительных конденсаторов Свх и Свых, вследствие чего образуются делители напряжения во входной и выходной цепях усилительного каскада. В результате уменьшается коэффициент передачи входной цепи и не все сформированное на коллекторе напряжение сигнала доходит до нагрузки. Анализ каскада в области нижних частот преследует цель получить расчетные соотношения для выбора емкостей разделительных конденсаторов по допустимой величине частотных искажений Mн на нижней граничной частоте fн для усилителей гармонических сигналов.
Оценим влияние разделительного конденсатора Cвх на коэффициент передачи входной цепи, воспользовавшись схемой входной цепи для области нижних частот (рис.2.31).
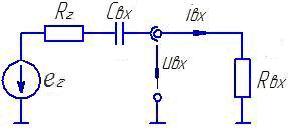
Рис.2.31. Эквивалентная схема входной цепи каскада для нижних частот
Полное сопротивление контура
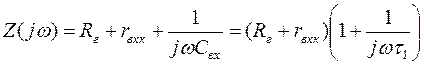 ,
,
где t1 = Cвх(Rг+rвх) – постоянная времени входной цепи на нижних частотах.
Коэффициент передачи входной цепи каскада
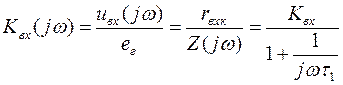 .
.
По последнему выражению можно записать соотношения для оценки вносимых конденсатором Cвх частотных и фазовых искажений
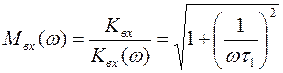 ;
;
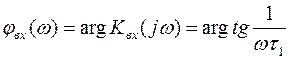 .
.
По допустимой величине частотных искажений Mвх на нижней рабочей частоте fн емкость конденсатора Cвх может быть выбрана из соотношения
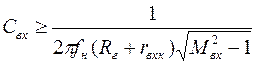 .
.
Значение Mвх в последнее выражение надо подставлять в относительных единицах, а не в децибелах. После расчета емкость конденсатора округляется до ближайшего стандартного номинала в большую сторону.
Схема выходной цепи каскада для области нижних частот, показанная на рис.2.32, позволяет по аналогии с рассмотренным ранее случаем получить частотную зависимость коэффициента передачи выходной цепи Kвых в виде соотношения
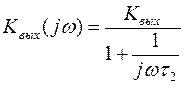 ,
,
где t2 = Cвых(Rн+Rвых) – постоянная времени выходной цепи каскада на нижних частотах.
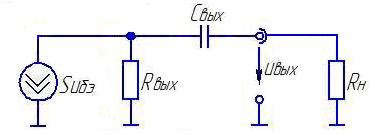
Рис.2.32. Эквивалентная схема выходной цепи каскада для нижних частот
Конденсатор Cэ на нижних частотах вносит дополнительные частотные искажения
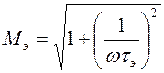 ,
,
где
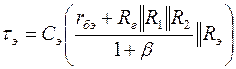 .
.
В области верхних частот учитывают влияние емкости коллекторного перехода Cк и инерционность процесса рекомбинации неосновных носителей, отражаемую комплексным коэффициентом передачи тока базы
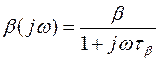 .
.
Эквивалентная схема замещения транзистора с общим эмиттером для области высоких частот, показанная на рис.2.11, может быть преобразована в эквивалентную схему замещения, показанную на рис.2.33. В этой схеме пренебрегли большим сопротивлением rкэ>>Rк. Величина емкости С1, включенной во входную цепь, определяется из условия сохранения тока во входной цепи в результате преобразования. В соответствии с рис.2.11 ток, протекающий через конденсатор Сбк со стороны базовой цепи равен
Imбк = wCбкUmбк.
В свою очередь напряжение
Umбк = Umбэ – Umбк = Umбэ + SUmбэRк .
Исходя из этого, ток во входной цепи останется неизменным, если между базой и эмиттером будет включена емкость C1 = Cбк(1 + SRк).
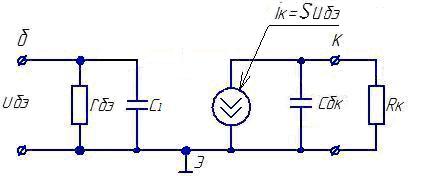
Рис.2.33. Эквивалентная схема каскада для области высоких частот
Ток со стороны коллекторной цепи, протекающий через емкость Cбк пропорционален разности (Umкэ – Umбэ), то есть Imкб = wCбкUmкб.
Преобразуя это соотношение, получим
Imкб = UmкэwCбк(1 + 1/SRк) » UmкэwCбк .
Из этого соотношения следует, что ток в выходной цепи не измениться, если между коллектором и базой будет включена емкость Cбк.
Легко показать, что наибольшее влияние на спад выходного сигнала, обусловленное шунтирующим влиянием емкости, будет оказывать входная цепь с емкостью C1. В результате ее действия с учетом инерции рекомбинации неосновных носителей частотная зависимость коэффициента усиления на высоких частотах примет вид
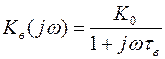 ,
,
где tв = tb + [rбэСбк(1+SRк)] – постоянная времени каскада в области верхних частот (первое слагаемое учитывает инерционность переноса носителей заряда в транзисторе, второе – влияние емкости коллекторного перехода).
Рассчитав постоянную времени в области высоких частот tв, можно оценить амплитудные и фазовые искажения на верхних частотах
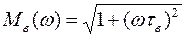 , jв(w)= - arctgwtв .
, jв(w)= - arctgwtв .
Объединяя результаты анализа в различных диапазонах частот, можно записать выражение для частотной характеристики сквозного коэффициента усиления в виде
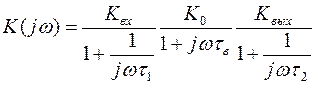 .
.
В последней формуле не учитываются искажения вносимые конденсатором, шунтирующим резистор RЭ, так как его влияние на частотные свойства, как правило, существенно меньше, чем влияние разделительных конденсаторов.
Амплитудно-частотная характеристика определяется выражением
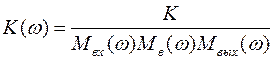 ,
,
где
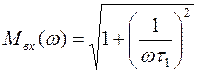 ;
; 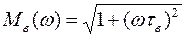 ;
; 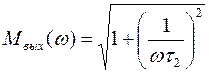 .
.
Фазочастотная характеристика каскада
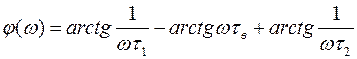 .
.
Ранее было показана связь между полосой пропускания усилителя (см.рис.1.2) и переходной характеристикой (см.рис.1.3). Чем больше полоса пропускания в области высоких частот, тем круче фронт импульса на выходе усилителя. Оценку длительного этого фронта можно определить по следующей формуле
tф = 2,2tв .
Величина спада переходной характеристики за время tи определяется нижней частотой полосы пропускания усилителя и может быть определена на основании выражения
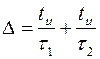 .
.
Дата добавления: 2018-11-26; просмотров: 2237;











