Теплопроводность через однослойную плоскую стенку
Дифференциальное уравнение теплопроводности позволяет определить температуру в зависимости от времени и координат в любой точке поля.
Для любого конкретного случая к нему надо присоединить необходимые краевые условия.
Рассмотрим наиболее распространенный случай — теплопроводность через однослойную плоскую стенку, длина и ширина которой бесконечно велики по сравнению с толщиной б (рис. 23-1). Стенка имеет во всех своих частях одинаковую толщину, причем температуры поверхностей t'cr и tcr поддерживаются постоянными, т. е. являются изотермическими поверхностями. Температура меняется только в направлении, перпендикулярном к плоскости стенки, которое принимаем за ось х. Коэффициент теплопроводности К постоянен для всей стенки. При стационарном тепловом режиме температура в любой точке тела неизменна и не зависит от времени, т. е.  Тогда дифференциальное уравнение теплопроводности после сокращения коэффициента температуропроводности принимает вид
Тогда дифференциальное уравнение теплопроводности после сокращения коэффициента температуропроводности принимает вид
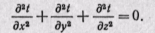
Но при принятых условиях первые и вторые производные от ( по y иz также равны нулю: 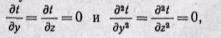
поэтому уравнение теплопроводности можно написать в следующем виде:
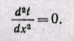 (23-1)
(23-1)
Интегрируя уравнение (23-1), находим

После вторичного интегрирования получаем
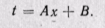
При постоянном коэффициенте теплопроводности это уравнение прямой линии. Следовательно, закон изменения температуры при прохождении теплоты через плоскую стенку будет линейным.
Найдем постоянные интегрирования А и В.
При х = 0 температура t = t'cr — B; при х = δ температура t = t"cr — Аδ +tст, откуда
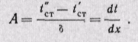
Плотность теплового потока найдем из уравнения Фурье (22-7)
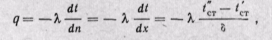
или
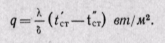 (23-2)
(23-2)
Зная удельный тепловой поток, можно вычислить общее количество теплоты, которое передается через поверхность стенки F за время τ:
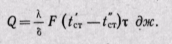 (23-3)
(23-3)
Количество теплоты, которое передается теплопроводностью через плоскую стенку, прямо пропорционально коэффициенту теплопроводности стенки К, ее площади F, промежутку времени т, разности температур на наружных поверхностях стенки (t'ст — t''ст) и обратно пропорционально толщине стенки δ. Тепловой поток зависит не от абсолютного значения температур, а от их разности
t'ст — t''ст = Δt наtзываемой температурным напором.
Полученное уравнение (23-2) является справедливым для случая, когда коэффициент теплопроводности является постоянной величиной. В действительности коэффициент теплопроводности реальных тел зависит от температуры и закон изменения температур будет выражаться кривой линией. Если коэффициент теплопроводности зависит от температуры в незначительной степени, то на практике закон изменения температур считают линейным.
Уравнение (23-2) можно получить непосредственно из закона Фурье (22-6), считая, что температура изменяется только в направлении оси х: 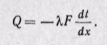
Разделив переменные, получаем
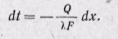
Интегрируя последнее уравнение при условии Q = const, находим 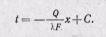
Постоянную интегрирования С найдем из граничных условий:
при х = 0 температура 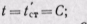
при х = δ температура 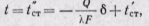 откуда
откуда
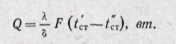
Введем в уравнение (23-2) поправки па зависимость λ от t, считая эту зависимость линейной:
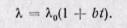 (а)
(а)
В этом случае, подставив в уравнение Фурье вместо К его значение из формулы (а), получаем
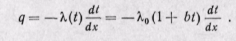 (б)
(б)
Разделив переменные и интегрируя в пределах от х = 0 до x = δ и в интервале температур от t'ст до t''ст, получаем
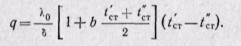 (23-4)
(23-4)
Полученное уравнение (23-4) позволяет определить плотность теплового потока при переменном коэффициенте теплопроводности. В этом уравнении множитель
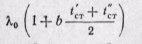
является среднеинтегралыюй величиной коэффициента теплопроводности.
В уравнении (23-2) было принято λ,=const и равным среднему значению λср. Поэтому, сравнивая уравнения (23-2) и (23-4), получаем
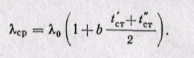 (23-5)
(23-5)
Следовательно, если λср определяется при среднеинтегральной температуре то формулы (23-2) и (23-4) равнозначны. 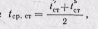
При этом плотность теплового потока может определяться из уравнения
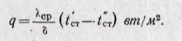 (23-6)
(23-6)
Интегрируя уравнение (б) в пределах от х — О до любой текущей координаты х и в интервале температур от t'ст ДО tx, получим уравнение температурного поля
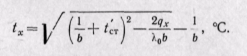 (23-7)
(23-7)
Из этого уравнения следует, что температура внутри стенки изменяется по кривой. Если коэффициент b отрицателен, то кривая будет направлена выпуклостью вниз; если b положителен, то выпуклостью вверх.
Дата добавления: 2016-06-29; просмотров: 2396;











