МЕТОДЫ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
В зависимости от природы процесса, от характера математической модели, от наличия информации о процессе, от постановки задачи применяются различные методы оптимизации процессов (табл. 22.1).
При решении конкретной задачи исследователь должен выбрать тот метод оптимизации, который при наименьших затратах на вычисления давал бы наибольший объем информации об искомом процессе.
Таблица 22.1
| Методы оптимизации | Характер процесса |
| I. Аналитические методы: аналитический поиск экстремума метод множителей Лагранжа вариационные методы принцип максимума Понтрягина | Детерминированные процессы, описываемые дифференцируе- мыми функциями с ограничени- ем и без ограничений |
| II. Методы математического программирования: геометрический линейный динамический | Детерминированные процессы с оптимизацией алгебраических функций |
| III.Градиентные методы | Детерминированные процессы с оптимизацией линейных и нели- нейных функций с ограничени- ем и без ограничения |
| IV. Автоматические методы с са- монастраивающимися моделями | Сложные объекты |
| V. Статистические методы: методы пассивного наблюдения (регрессионный и корреляционный методы анализа) методы активной оптимизации Метод Бокса - Уилсона и др. | Стохастические процессы |
Дадим краткую характеристику наиболее часто применяющимся методам оптимизации для детерминированных процессов. Методы исследования функций с помощью классического анализа являются наиболее известными способами решения несложных задач оптимизации.
Эти методы применяются для решения задач с известным аналитическим выражением критерия оптимальности, Приравнивая нулю производные и решая конечную систему уравнений, определяют экстремальные значения параметра оптимизации.
Метод множителей Лагранжа используется для решения таких же задач, как и задач, решаемых методом исследования функций, но при наличии ограничений на независимые переменные. Порядок системы уравнений, которые решаются при нахождении экстремумов параметра оптимизации, повышается на число ограничений. В остальном процедура поиска решений аналогична.
Методы вариационного исчисления обычно применяют для решения задач с критерием оптимальности в виде функционалов. Вариационными методами решение задачи сводится к интегрированию системы дифференциальных уравнений Эйлера второго порядка с граничными условиями. Число уравнений системы равно числу неизвестных функций.
Динамическое программирование является эффективным методом решения задач оптимизации дискретных многостадийных процессов, для которых общий критерий оптимизации является функцией критериев оптимальности, отдельных стадий.
Принцип максимума Понтрягина применяется для оптимизации процессов, описываемых системами дифференциальных уравнений. Оптимальное решение находится путем интегрирования системы дифференциальных уравнений процесса и системы вспомогательных функций с ограничением на обоих концах интервала интегрирования.
Линейное программирование используется для решения задач оптимизации с линейным выражением для критерия оптимальности и линейными ограничениями на область изменения переменных факторов. Это задача оптимального планирования производства с ограниченным количеством ресурсов, транспортные задачи и др. Универсальный алгоритм решения задач линейного программирования содержится в симплексном методе, позволяющем за конечное число операций найти оптимальное решение большинства задач.
Методы нелинейного (динамического) программирования применяют для решения задач оптимизации с нелинейными функциями параметра оптимизации с ограничениями и без ограничений на независимые переменные.
Для оптимизации стохастических процессов используются экспериментально-статистические методы. Различают пассивный и активный эксперимент. Пассивный эксперимент, или, как его часто назьюают, пассивное наблюдение, использует методы математической статистики для обработки информации с целью изучения закономерностей технологического процесса. При этом сбор исходных данных проводится на действующем объекте без введения в процесс искусственных изменений. Обработка данных с целью получения математической модели процесса проводится в основном методами классического регрессионного и корреляционного методов анализа.
Активный эксперимент основан на применении планирования эксперимента. Планирование эксперимента — это проведение эксперимента по заранее составленному плану (матрице), обладающему оптимальными свойствами. При планировании учитываются одновременно все факторы, влияющие на процесс, что позволяет выявить сразу и силу взаимодействия факторов, и резко сократить общее число опытов для определения оптимальных параметров. Как в пассивном, так и в активном эксперименте математической моделью является функция отклика, связывающая параметр оптимизации с факторами, влияющими на процесс:
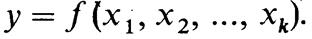
При использовании статистических методов математическая модель представляется в виде отрезка ряда Тейлора. Уравнение регрессии имеет вид
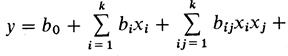
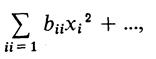
где b0 — свободный член уравнения регрессии; bi — линейные коэффициенты; bji — коэффициенты взаимодействия; bii — квадратичные коэффициенты.
Коэффициенты уравнения определяются методом наименьших квадратов (МНК) из условия
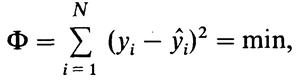
где N— объем выборки; уi — соответственно экспериментальное и теоретическое значения параметра оптимизации.
Дата добавления: 2016-06-22; просмотров: 3921;











