ОБЩАЯ ПОСТАНОВКА ЗАДАЧ ОПТИМИЗАЦИИ ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
Современные технологические процессы — обычно многостадийные, протекающие с высокими скоростями, при высоких температурах и давлениях в многофазных системах, — характеризуются сложностью и многообразием операций и оборудования.
Продукцию высокого качества можно получать лишь при поддержании строго определенных технологических режимов. Применявшиеся ранее для изучения многофакторных технологических процессов однофакторные методы не гарантировали оптимальности найденных режимов и требовали для их реализации длительного времени.
В последние годы для оптимизации сложных процессов широкое распространение получили статистические методы планирования эксперимента. Конечной целью исследования является получение адекватной математической модели процесса и нахождение оптимального технологического режима. Математические модели позволяют не только оптимизировать сами процессы, но и оптимально управлять ими при изменении отдельных параметров. Кроме того, математические модели процессов являются источником информации для создания автоматизированных систем управления технологическим процессом (АСУТП).
При применении статистических методов планирования для оптимизации технологических процессов используется понятие «черного ящика», заимствованное из кибернетики*[11]. Математическая модель, построенная исходя из экспериментальных данных, используется для разработки оптимальных режимов. Эксперимент осуществляется по определенному плану в соответствии с теорией планирования эксперимента. Общее число опытов невелико. При неполном знании механизма процесса статистические методы оптимизации являются весьма эффективными. Основоположником статистического планирования эксперимента является английский ученый Р. Фишер. Современная форма планирования эксперимента в СССР начала развиваться с 1900-х годов.
Оптимизация — это целенаправленная деятельность человека, заключающаяся в получении наилучших результатов при соответствующих условиях.
Для правильной постановки задачи оптимизации необходимо, чтобы выполнялись следующие условия:
а) существовал объект оптимизации (технологический процесс) с управляющими воздействиями (факторами), которые позволяют изменять его состояние в соответствии с требованиями;
б) должна быть правильно сформулирована цель оптимизации, при этом оптимизации подвергается только одна величина;
в) оптимизируемая величина должна иметь количественную оценку. Количественная оценка оптимизируемого объекта называется критерием или параметром оптимизации.
Вид критерия оптимизации определяется конкретной задачей. Наиболее общим критерием оптимальности являются экономические оценки. Общая оценка экономической эффективности процесса (R) включает следующие показатели:
производительность В, численно выражаемая объемом выпускаемой продукции в единицу времени; объем копи-талъных вложений Ф в данное производство; эксплуатационные затраты Э на осуществление процесса; количественный показатель К выпускаемого продукта.
В общем случае экономический критерий оптимальности процесса является функцией от этих показателей:
R = f(В, Ф, Э, K).
Одним из важнейших показателей экономической эффективности процесса является себестоимость выпускаемой продукции, которая включает стоимость сырья, материалов, топлива, энергии, переменные и постоянные расходы.
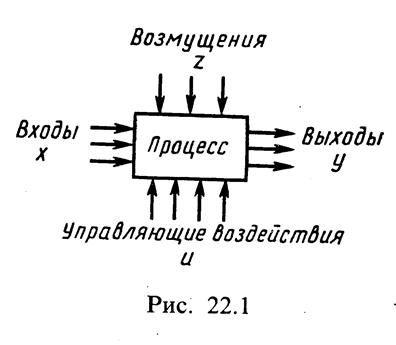
Любой технологический процесс может быть условно изображен так, как показано на рис. 22.1, на котором выделены основные группы параметров, которые определяют состояние процесса:
входные факторы х1, х2, ..., хк. Они измеряемы, контролируемы, но воздействовать на них нельзя. Значения их не зависят от режима процесса: например, состав исходного сырья, не поддающийся измерению в эксплуатации;
управляющие факторы и1, и2, ..., иr, на которые можно воздействовать для управления процессом: например, количество исходного сырья, давление, температура и другие факторы;
возмущающие факторы z1, z2, ..., zl, значения которых случайным образом изменяются во времени и не поддаются измерению, например содержание различных примесей в исходном сырье, изменение активности катализатора и др.;
выходные параметры у1у2, ... , Уn, значения которых определяются состоянием процесса, возникающим в результате воздействия входных параметров, т. е. общего действия входных факторов, возмущений и управляющих воздействий.
При решении задач оптимизации процессов выходные параметры чаще всего являются технологическими или технико-экономическими. Если все выходные параметры процесса обозначить через Y-критерий оптимизации, а все исходные параметры через X, Z, U, то процесс моделирования сводится к установлению вида математической зависимости между выходными и входными параметрами:
Y = f (X, Z, U).
Математическая модель количественно отражает сущность явлений, протекающих в технологическом процессе.
С помощью определенного алгоритма математическая модель дает возможность прогнозировать поведение объекта (технологического процесса) при изменении входных параметров.
Математическое моделирование технологического процесса включает три стадии: 1) построение математической модели; 2) алгоритмизация для нахождения числовых значений параметров; 3) установление адекватности (соответствия) математической модели изучаемому процессу.
Адекватная модель — это такая модель процесса, которая с достаточным приближением качественно и количественно описывала бы данный процесс.
Адекватность модели устанавливается или физическим путем, или математически. Вид модели определяется природой изучаемых процессов.
По своей природе технологические процессы подразделяются на детерминированные и стохастические.
Детерминированным называется процесс, в котором определяющие величины изменяются непрерывно, но вполне по определенным закономерностям. Значение выходной величины однозначно определяется значением входной. Для описания детерминированных процессов применяются методы классического анализа и численные методы. Например, любой физический массообменный или теплообменный процесс является детерминированным.
Стохастическим называется такой процесс, в котором изменение определяющих величин происходит беспорядочно и часто дискретно. При этом значение выходной величины не находится в соответствии с входной. Для описания таких процессов используют вероятностно-статистические методы. Примером может быть любой каталитический процесс, в котором выход продукта изменяется от падения активности катализатора в течение процесса.
Дата добавления: 2016-06-22; просмотров: 3413;











