Регрессионный и корреляционный методы анализа при оптимизации технологических процессов
Эти методы широко применяются в технико-экономических исследованиях для:
установления зависимости между свойствами продукции и технологическими факторами ее изготовления;
установления связи между некоторыми характеристиками, которые определяют условия эксплуатации изделий;
изучения взаимосвязи между факторами технологического процесса, а также между факторами и технико-экономическим параметром оптимизации процесса.
Корреляция — это статистическая зависимость, проявляющаяся, когда результат опыта зависит не только от исследуемых факторов, но и от ряда других меняющихся условий. Парная корреляция изучает зависимость параметра от одного фактора, множественная — от нескольких факторов. Оптимизация технологических процессов с помощью корреляционного метода проводится по этапам.
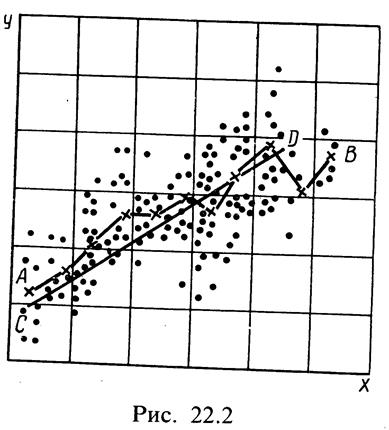
На первом этапе устанавливается наличие корреляционной связи между изучаемыми признаками, например между фактором х и параметром оптимизации у. Для этого исходные данные представляются в виде корреляционного поля точек с координатами х и у (рис. 22.2).
На втором этапе определяют форму связи. С этой целью производят расчет эмпирической и теоретической линии регрессии. Для построения эмпирической линии регрессии на основании корреляционной таблицы определяют средние значения параметра оптимизации у для каждого интервала разбиения:
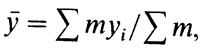
где у — среднее значение параметра у в интервале ∆х(; yf — среднее значение у по интервалам ∆yt; m — число точек в интервалах ∆xi и ∆yi.
Ломаная линия АВ (рис. 22.2), соединяющая точки (xiyi) отрезками, называется эмпирической линией регрессии.
По виду эмпирической линии строят и определяют теоретическую линию регрессии CD [в случае прямолинейной зависимости по уравнению
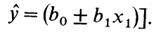
Коэффициенты bo и b1 определяют с помощью МНК, решая систему нормальных уравнений для выборки N значений:
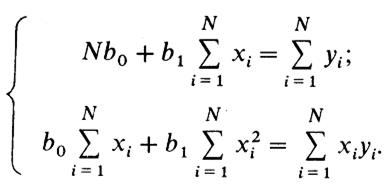
На третьем этапе определяют тесноту связи между величинами х и у. Для этого вычисляют коэффициент парной корреляции:
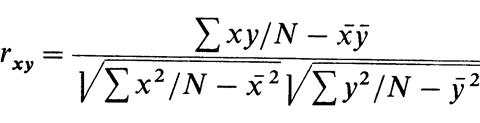
Величина rху показывает силу связи между параметрами х и у. Исследование полученного уравнения проводится методом регрессионного анализа и сводится к установлению адекватности уравнения и оценки значимости коэффициентов уравнения.
Адекватность уравнения при наличии параллельных опытов проводится по критерию Фишера:
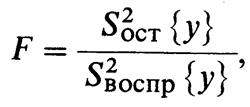
где Soct {у} — остаточная дисперсия; £воспР {у} — дисперсия воспроизводимости.
Числовые значения дисперсий определяют по формулам
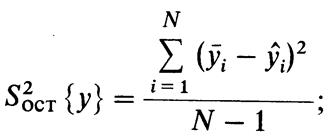
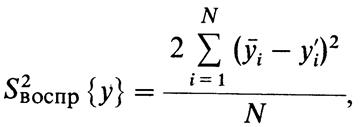
где yt — теоретическое значение параметра оптимизации; yf — среднее значение параметра оптимизации, взятое из п = 2 параллельных опытов; y′i — значение параметра оптимизации в одном из п = 2 параллельных опытов.
Если Fэкс < Fтабл (f1, /2), то уравнение адекватно представляет результаты эксперимента.
Оценка значимости коэффициентов математической модели проводится по критерию Стьюдента t:
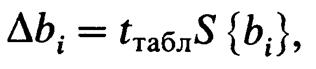
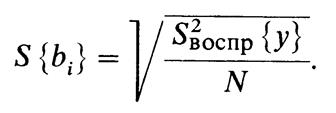
Если ׀bi׀> ∆bi,то коэффициент F значим.
Адекватность полученного уравнения говорит о возможности использовать уравнения для приближенных расчетов параметра оптимизации у по заданным факторам xt.
К недостаткам методов пассивного наблюдения следует отнести: а) необходимость большого количества информации для получения достоверных данных; б) интерполяционный характер математической модели, т. е. она справедлива лишь для исследуемого интервала изменения факторов xi.
Однако способ пассивной оптимизации является экономически эффективным при оптимизации реального непрерывного процесса. Пассивная оптимизация является подготовкой к активному эксперименту.
Методы планирования эксперимента для оптимизации технологических процессов
Методы планирования эксперимента начали успешно развиваться и применяться с 1960-х годов в связи с внедрением комплексной автоматизации производственных процессов и ЭВМ. Методы планирования эксперимента называют часто активным экспериментом. Эти методы позволяют разработать алгоритм оптимального управления технологическим процессом. К преимуществам этого метода относят минимальное требуемое число опытов, чтобы получить математическую модель и установить оптимальную область параметра оптимизации. В отличие от классического эксперимента, где каждый изучаемый фактор исследуется отдельно, в активном эксперименте все факторы изменяются сразу и причем целенаправленно.
В настоящее время в планировании эксперимента можно выделить следующие направления:
оптимизация многофакторного экстремального эксперимента (метод Бокса — Уилсона);
эксперимент в «почти стационарной области»;
отсеивающий эксперимент;
эксперимент с качественными факторами;
симплексный метод планирования эксперимента;
эволюционное планирование экспериментов.
Из перечисленных методов наибольшее распространение для оптимизации многофакторных экстремальных технологических процессов имеет метод Бокса — Уилсона. При оптимизации какого-либо технологического процесса по этому методу зависимость между выходом у и входами хi можно записать так:
y = f(x1, х2, ... ,хк).
Геометрически эта функция отклика представляет собой поверхность, на которой необходимо найти экстремальное значение. Поверхность должна быть непрерывной и гладкой и иметь один оптимум.
В методе Бокса — Уилсона выделяют два этапа:
1) поиск оптимальной области — «крутое восхождение»;
2) описание «почти стационарной» области. Стратегия поиска оптимума заключается в последовательной постановке небольших серий опытов по матрице планирования.
Для построения матриц планирования используется факторный анализ, а для построения математической модели — регрессионный анализ.
Эксперимент обычно осуществляется по матрице полного факторного эксперимента (ПФЭ) с числом опытов N = 2к , где к — число факторов с числом уровней факторов, равным двум, или по матрице дробного факторного эксперимента (ДФЭ) с числом опытов N = 2к-1; N= 2k-2 и т, д.
ПФЭ — это реализация всех возможных комбинаций из к факторов. Например, для к = 2 число опытов будет N = 22 = 4. Матрица планирования в кодированном виде представлена в табл. 22.2.
Таблица 22.2
| Номер опыта | x0 | x1 | x2 | y |
| + 1 | + 1 | + 1 | y1 | |
| + 1 | - 1 | - 1 | y2 | |
| + 1 | + 1 | - 1 | y3 | |
| + 1 | - 1 | +1 | y4 |
Используя регрессионный метод анализа исвойства матриц планирования (симметричность, ортогональность, нормировка), определяют коэффициенты уравнения регрессии по формулам
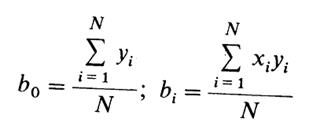
и строят линейную математическую модель
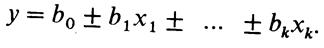
Далее проводят статистический анализ уравнения, проверяют на адекватность. После статистического анализа уравнения производят интерпретацию уравнения, которая сводится к оценке влияния значимых факторов на параметр оптимизации. Принятие решений после построения и интерпретации модели процесса зависит от числа факторов, дробности плана, цели исследования, адекватности модели, значимости факторов, информации о положении оптимума. Например, если линейная модель адекватна, а область оптимума не достигнута, то проводят «крутое восхождение».
Крутое восхождение — это движение по наиболее короткому пути в направлении градиента функции. Движение по градиенту реализуют до тех пор, пока улучшается значение параметра оптимизации. Если достигнуть оптимума не удается, то ставят новую серию опытов и определяют новое направление движения по градиенту. Такой «шаговый» процесс продолжают до тех пор, пока исследователь не попадает в «почти стационарную» область, где линейное приближение оказывается неадекватным. Координаты опытов в крутом восхождении рассчитывают путем прибавления к основному уровню «шага» размером biJi где bi — коэффициент регрессии уравнения, a Ji — интервал изменения фактора. Крутое восхождение считается эффективным, если хотя бы один из реализованных опытов даст лучший результат по сравнению с наилучшим результатом опыта в серии. После крутого восхождения принимают решения о дальнейшей оптимизации процесса. Например, если оптимальная область достигнута, то эксперимент заканчивают. Метод позволяет определить математическую модель процесса и оптимум параметра оптимизации.
* Маркс К., Энгельс Ф. 2-е изд., т. 23, с. 383.
** Там же, с. 191.
* Маркс К., Энгельс Ф. Соч. 2-е изд., т. 47, с. 461
** Маркс К., Энгельс Ф. Соч. 2-е изд., т. 4, с. 152
* Ленин В. И. Поли. собр. соч., т. 5, с. 125.
* Маркс К., Энгельс Ф.Соч. 2~е изд., т. 46, ч. II, с. 213.
* В атмосфере над 1 га поверхности земли находится до 80 тыс. т азота.
** При переходе от агрегатов мощностью 120 т/сут к агрегатам мощностью 1360 т/сут себестоимость аммиака снижается на 60%, а производительность труда увеличивается в 7,2 раза.
* В этой реакции число молей конечных продуктов (1+4 = 5) больше числа молей исходных реагентов (1 + 1=2), что указывает на ее протекание с увеличением объема.
* Световой поток состоит из отдельных порций энергии — фотонов
* Ленин В. И. Поли. собр. соч., т. 36, с. 188.
* В последние годы производство простого суперфосфата как низкоконцентрированного и малоперспективного удобрения непрерывно сокращается, а производство двойного суперфосфата увеличивается.
* В кибернетике под «черным ящиком» понимают устройство, выполняющее некоторую операцию по преобразованию входных переменных в выходные параметры.
Дата добавления: 2016-06-22; просмотров: 3236;











